Proszę pomóżcie :( kuba: w trójkącie abc dane są cosinus przy wierzchołku A= −8/15, cosinus przy wierzchołku B =4/5 i bok AB=24. Oblicz długość pozostałych boków trójkąta. Próbowałem to zrobić na dwa twierdzenia cosinusów ale nie wychodzi mi już od 30 minut

kuba: ktoś pomoże?

Janek191:

	8
cos α = −
	15

	4
cos β =
	5

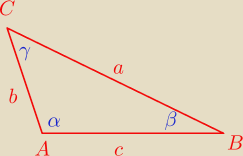
c = 24

kuba: tak rysunek dobry ale tyle to i ja umiem

kuba: proszę nadal o pomoc

Eta: Masz odp do tego zadania? Czy dobrze podałeś dane? ( bo wyniki wychodzą niezbyt ciekawe

x: Rób przez tw. sinusów...

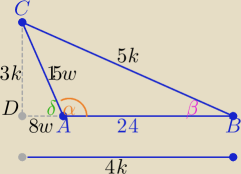
Eta: Można tak:( łatwiejsze obliczenia niż dwa razy z tw. kosinusów)

	8
cosδ= −cosα=
	15

	4
cosβ=		to |DB|=4k i |BC|=5k i |DC|=3k , k>0
	5

	8
w trójkącie DAC : cosδ=		to : |AD|=8w, |AC|=15w , w>0
	15

to |DC|=3k=U{√225w²−64w²=√161*w 4k=8w+24 ⇒ k=2w+6 ⇒ 3k=6w+18

	18
√161w−6w=18 ⇒ w=		(√161+6)
	125

zatem:

	54
|AC|=15w= ............=		(√161+6)
	25

	5		6
|BC|= 5k=		√161*w= .........=		(161+6√161)
	3		25

P.S. kuba dostałeś to zadanie za jakieś ciężkie przewinienie?

Eta: A tak prosił o pomoc i............