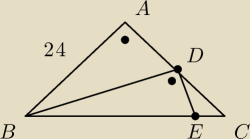
geometria Kacper: Zadanko dla chetnych Wiadomo, że ΔABC − równoramienny prostokątny oraz punkt D −środek odcinka AC. Reszta na rysunku. Oblicz pole trójkąta CDE

Benny: P=24?

Eta:

Benny: Czekam aż pokażesz jakieś krótkie rozwiązanie

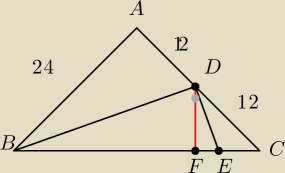Saizou : Łatwo obliczyć odcinki |BF|=18√2 |CF|=|DF|=6√2 z podobieństwa trójkątów ΔBDF~ΔDEF (kk) mamy że

|DF|		|EF|
	=
BF||		|DF|

6√2		|EF|
	=		⇒|EF|=2√2
18√2		6√2

zatem |CE|=6√2−2√2=4√2, wówczas

	1
PCDE=		•6√2•4√2=24
	2

Eta:

Saizou : Etuś albo Kacper masz może jeszcze jakieś prostsze rozwiązanie ?

Eta: [BFD]=108 , [FCD]=36, [EFD]=k²*108

	6√2		1
k=		=		to [EFD]= 12
	18√2		3

zatem [CED]=36−12=24 j²

bezendu: Eta ?

Eta: Ooo już się nie gniewasz na mnie? Wybieram to po lewej

bezendu: A czy ja się na Ciebie kiedyś gniewałem ? Za tyle pomocy jaką od Ciebie dostałem, to ja Ci będę wdzięczny do końca życia !

Eta:

Kacper: Wrzucę później inne rozwiązanie bez pierwiastków Trudniej na nie wpaść, ale mnie się podoba

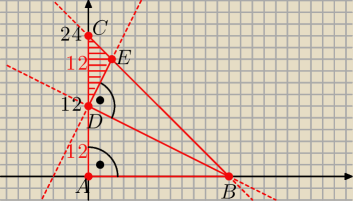Bogdan: Szkic. A = (0, 0), B = (24, 0), C = (0, 24), D = (0, 12),

	1
prosta BC: y = −x + 24, prosta BD: y = −		x + 12, prosta DE: y = 2x + 12
	2

x_E: 2x_E + 12 = −x_E + 24 ⇒ x_E = 4, wysokość trójkata CDE z wierzchołka E jwst równa 4

	1
Pole trójkata CDE: P =		* 12 * 4 = 24
	2

Eta:

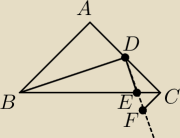Kacper: Na przedłużeniu boku DE trójkąta CDE obieramy taki punkt F, że trójkąt FCD jest podobny do

	1
trójkąta ABD w sklali		.
	2

	PΔFCD		1
Wynika stąd, że		=		.
	PΔABD		4

	PΔFCE		1
Ostatnim krokiem jest zauważenie, że		=		, zatem
	PECD		2

	2
PΔCDE=		*PΔFCD.
	3

	1
Ostatecznie PΔCDE=		PΔABD=24
	6