Ile rozwiązań rzeczywistych ma równanie marcylka: Ile rozwiązań rzeczywistych ma równanie (x2−4x+3x)√4−x2 = 0 (√4−x2 jest całe pod pierwiastkiem).

ZKS: Zapisz to porządnie.

J: (..........)*√4−x² = 0 ... zgaduję

marcylka: (x2−4x+3x) √4−x2 = 0

J: .. no to ... nawias = 0 lub √4−x² = 0 ... i działaj...

marcylka: √4−x² = 0

marcylka: tzn?

J: x² − 4x + 3 = 0 ... równanie kwadratowe √4−x² = 0 ⇔ 4 − x² = 0 ⇔ x² = 4 ⇔ .....

marcylka: delta 28, x₁= 4− √28 przez 2. ( nie potrafię zapisać 2 w mianowniku , sorki −.− x₂=4+√28 przez 2

marcylka: a z √4−x2 = 0 wychodzi 2

marcylka: a więc ma 3 rozwiązania tak?

ZKS: Dziedzina najpierw.

marcylka: dziedziną jest zbiór licz rzeczywistych

J: a jakim sposobem masz : Δ = 28 ?

J: nie... musi być warunek: 4 − x² ≥ 0 ⇔ ..... ?

marcylka: a fakt, delta = 4

marcylka: nie rozumiem co zroibć z 4 − x2 ≥ 0 ⇔ ..... ?

marcylka: x₁=1 x₂= 3

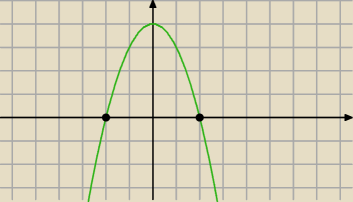
J: odczytaj z wykresu kiedy: 4 − x² ≥ 0

marcylka: dalej nie ogarniam jak mam odczytać?

J: dla jakich x , wykres leży nad osią OX lub ją przecina ?

marcylka: dla xów dodanich i xów ujemnych, założmy ze w przedziale (−1,1)

J: x ∊ <−2,2>

marcylka: ok no i właściwie po co mi to ?

J: rozwiązania równania muszą należeć do tego przedziału

Metis: Podnosisz obustronnie do kwadratu, potrzebne założenia, stąd 4 − x ≥ 0

J: zauważ,że x = 3 nie należy do tego przedziału, więc nie może być rozwiązaniem równania ( nie należy do dziedziny)