Konstrukcja odcinka √a mwil25: Jak skonstruować odcinek o długości √a korzystając z twierdzenia Talesa?

pigor: ... , każdy chyba wie, że jest to odcinek długości przekątnej kwadratu o boku 1, a tu może warto zauważyć, że jeśli x=? − dl. szukanego odcinka, to mamy proporcję

	2		2		x
√2=x i x>0 ⇒ 2=x2 /:x ⇒		= x ⇔		=		...
	x		x		1

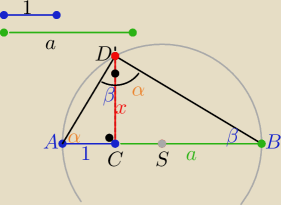Eta: W tym zadaniu należało skonstruować odcinek x= √a a nie jak podał pigor x= √2 Z podobieństwa trójkątów ACD i BCD :

x		a
	=		⇒ x2=a ⇒ |CD|=x=√a
1		x

AS: Zgoda,tylko rozwiązanie miało być wykonane stosując tw. Talesa.