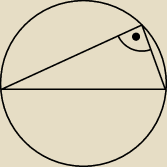
Zbior wartosci sss: Trojkat prostokatny o jednj z przyprostokatnych dlugosci x jet wpisany w okrag o promieniu 5. Podaj wzor funkcji opisujacej pole tego trojata w zaleznosci od x. Wyznacz dzidzine i zbior wartosci tej funkcji.

	1
funkcje obliczylem − y=		x(√100−x2 Dziedzina to 0 i 10. Ale jak obliczyc zbior
	2

wartosci?

Godzio: Dziedzina to 0 i 10? Co to oznacza? Pochodne znasz?

Marek:

sss: Nie znam pochodnych. Zle napisalem dziedzina (0,10)

Anita Berg: Pochodna i całka funkcji − niebieska woń w menu po lewej stronie.

sss: ale to jest w ksiazce do 1 klasy technikum...

Eta: f(x)=0,5√x²(100−x²) D_f= (0,10) z nierówności między średnimi am−gm

	a+b
mamy 0< √ab≤
	2

	1		1		x2+100−x2		100
to 0<		√x2(100−x2≤		*		=		=25
	2		2		2		4

ZW=(0,25>

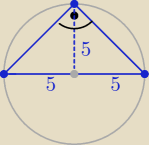
Eta: Można też tak:( najłatwiej Największe pole ma trójkąt prostokątny równoramienny o podstawie 2r=10 pole takiego trójkąta jest równe 25 zatem ZW=(0,25>

pigor: ..., lub y= ¹₂x√100−x² i 0<x<10 i y>0 ⇒ 2y= x√100−x² ⇒ ⇒ 4y²=x²(100−x²) ⇔ x⁴−100x²+4y²= 0 i Δ ≥0 i y >0 ⇒ ⇒ 00²−16y² ≥0 i y >0 ⇔ 4|y| ≤ 100 i y >0 ⇔ 0< y ≤ 25 ⇔ ⇔ y∊ (0; 25> =Z.W.. ...

pigor: ..., jeśli miał Δ (deltę) i warunek istnienia miejsc zerowych funkcji kwadratowej. ...

Eta: W kl.1 nie zna jeszcze delty ( funkcja kwadratowa dopiero w 2 kl

pigor: ..., niektórzy − zwłaszcza w technikum − np. z racji przedmiotów zawodowych zapoznawani są z f. kwadratową i "deltą" już w I−szej klasie ....