zadaa himenaa: Hej Jak rozwiązywać równania i nierówności liniowe z parametrem. Np: 1) Określ liczbę rozwiązań danego równania w zależności od wartości parametru a. Dla tych wartości parametru a dla których istnieją rozwiązania podaj te rozwiązania : ax + 5 = 5x − a 2) − I I − − II − w zalezności od wartości parametrów a i b. − II − ( to samo polecenie ) a) ax − 3 = x + b I jeszcze jak rozwiązywać równania i nierówniści z wartością bezwzgl : To tak na przykładzie a) I x − 1 I + I x + 3I = 4

J: 3) Rozwiązujesz w przedzialach (−∞,−3) [−3,1) [ 1,+∞) Jezeli w danym przedziale liczba pod wartością bezwzględną jest ujemna, to zmieniasz jej znak np. w ( − ∞,−3 ) I x − 1I = − x + 1

J:

	− a − 5
1) ax − 5x = − a − 5 ⇔ x(a − 5) = − a − 5 ⇔ x =		,
	a − 5

dla: a = 5 ... brak rozwiązań dla: a ≠ 5 ... jedno rozwiązanie

Godzio: Zad 1 1. Wyliczasz x ax + 5 = 5x − a 5x − ax = 5 + a x(5 − a) = 5 + a

	5 + a
x =		gdy a ≠ 5
	5 − a

Gdy a = 5 mamy x * 0 = 5 + 5 ⇒ 0 = 10 sprzeczność

	5 + a
Gdy a ≠ 5 mamy jedno rozwiązanie x =
	5 − a

Często bywa też tak, że pojawia się przypadek gdy dla pewnego 'a' otrzymujemy 0 = 0, wówczas mamy nieskończenie rozwiązań. Zad 2 ax − 3 = x + b ax − x = b + 3 x(a − 1) = b + 3

	b + 3
x =		dla a ≠ 1 i dowodnego b mamy jedno rozwiązanie
	a − 1

Gdy a = 1 i b ≠ − 3 mamy sprzeczność ( 0 = b + 3 ≠ 0 ) Gdy a = 1 i b = − 3 mamy nieskończenie wiele rozwiązań. Zad 3 kto inny wyjaśni bo już się nie wyrobię

himenaa: Dzięki !

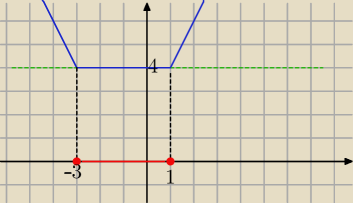Eta: x=<−3,1> −−− nieskończenie wiele rozwiązań

pigor: ... I jeszcze pytasz jak rozwiązywać równania i nierówności z wartością bezwzględną : na przykład a) Ix−1I+Ix+3I= 4 no to tu proponuję najlepiej tak : ..., rysujesz sobie punkty x=1 i x= −3 na osi OX i masz przedział <−1,3> teraz stawiasz długopisem kropkę w dowolnym punkcie tego przedziału i co widzisz , ano, że każdy taki punkt x∊<−3;1> przedziału spełnia dane równanie − szukany zbiór rozwiązań danego równania, koniec , bo właśnie suma jego odległości od końców tego przedziału <−3;1>. jest faktycznie równa 4, oczywiście warto się przekonać, że postawiona kropka (wartość x) długopisem poza tym przedziałem już nie spełnia danego równania, bo ta suma jest >4, a więc jeśli już to np. |x−1I+Ix+3I > 4 ⇔ ... x∊(−∞;−3)U(4;+∞) itp., itd.

daras: a ja proponuję wpisac w tutejszą wyszukiwarkę i rozwiązac albo chociaż zobaczyć rozwiązania licznych przykładów, które tutejsi rzemieślnicy rozwalili w bierzącycm stuleciu http://www.google.pl/cse?cx=partner-pub-8082496537969329%3Amqxxzmak47q&ie=UTF-8&q=r%C3%B3wnania+z+warto%C5%9Bci%C4%85+bezwzgl%C4%99dna+z+parametrem+&sa=Szukaj&siteurl=matematyka.pisz.pl%2Fstrona%2Fszukaj.html&ref=matematyka.pisz.pl%2Fstrona%2F3412.html&ss=16648j9191968j62#gsc.tab=0&gsc.q=r%C3%B3wnania%20z%20warto%C5%9Bci%C4%85%20bezwzgl%C4%99dna%20z%20parametrem&gsc.page=1

Eta: Racja wreszcie opalony daras

himenaa: Dziękuje wszystko fajnie tylko nie rozumiem w drugim zadaniu z parametrem a i b tych rozwiązań tego równania tzn. na pewno wiem ze mianownik musi być różny od 0 ale ta trójka mnie myli..

J: Jeśli a = 1 i b ≠ − 3 ...dostajemy sprzeczność ( dzielenie konkretnej liczby przez zero )

	0
Jeśli a = 1 i b = − 3 ... dostajemy symbol nieoznaczony [		] .. .co oznacza,że równanie ma
	0

nieskończenie wiele rozwiązań