Zadanie nr 118. 5-latek: Zadanie : Rozwiaz równanie ⁿ√(x+1)² +ⁿ√(x−1)²= 4√x²−1 gdzie n jest liczba naturalna jak się do tego zabrać ?

5-latek: Ma być =4ⁿ√x²−1 .

Saizou : ⁿ√(x+1)²−2ⁿ√x²−1+ⁿ√(x−1)²−2ⁿ√x²−1=0 (ⁿ√x+1−ⁿ√(x−1))²−2ⁿ√x²−1=0 dasz teraz radę ?

5-latek: Zaraz to przemysle

5-latek: Niestety nie dam rady gdyż nie wiem jak będzie wygladac pierwiastek z 2ⁿ√x²−1 Tutaj z tego co widze należy skorzystać ze wzoru x²−y² wiec nasze x= (ⁿ√x+1−ⁿ√x−1) ale jak będzie wygladac y?

5-latek: czy to będzie tak ze y= √2ⁿ√x²−1 = √2*p2n{x²−1}? Ten drugi pierwiastek to jest stopnia 2n

5-latek:

henrys: hmmm, ciekawe możliwe żeby było coś takiego?

	(2−√3)n+1
x=
	(2−√3)n−1

henrys:

	(2+√3)n+1
drugie rozwiązanie: x=
	(2+√3)n−1

5-latek: W odpowiedzi mam ze dla n parzystego 1 rozwiązanie dlan nieparzystego 2 rozwiązania . Zostawie to na jutro . Dobranoc

henrys: ok dzięki

henrys: weźmy n=2 √(x+1)²+√(x−1)²=4√x²−1 |x+1|+|x−1|=4√x²−1 x∊(−∞,−1>u<1,∞) 1^o x≥1⇒x+1+x−1=4√x²−1 2x=4√x²−1 x=2√x²−1/² x²=4x²−4

	2√3
x=		ok
	3

2^o x≤−1⇒−x−1−x+1=4√x²−1 −2x=4√x²−1 −x=2√x²−1/² lewa i prawa strona są dodatnie x²=4x²−4

	−2√3
x=		ok
	3

Mamy więc dwa rozwiązania dla n parzystego, to nie wiem co z tą odpowiedzią, chyba że się gdzieś pomyliłem W ogóle to dla x=1 lub x=−1 równanie nie jest spełnione więc te nierówności słabe można zamienić na ostre.

5-latek: Nie chciałem robic jak jest w podpowiedzi . Ty doszsedles według tej podpowiedzi do dobrych wzorow Bo tak oznaczmy u=ⁿ√x+1 i v=ⁿ√x−1 ============================ Z warunków zadania dostaniemy związek (1) u²+v²= 4u*v ================ latwo wykazac ze żadna z liczb u i v nie może być zerem (latwo Z równania (1) wynika z eiloczyn u*v musi być dodatni. dzieląc równanie (1) przez v² otrzymujemy

	u		u
(		)2−4		+1=0
	v		v

===================

	u
skad		= 2+ε√3 gdzie ε=±1 (to weim bo Δ=12 i √12= 2√3
	v

Z drugiej strony

u		x+1
	= n√
v		x−1

===================== Otrzymujemy wiec równanie

x+1
	= (2+ε√3)n
x−1

	(2+ε√3)n+1
stad (2) x=
	(2+ε√3)n−1

Ty otrzymales takie same ale dwa równania Przeprowadzmy dyskusje naszego zadania > Przypadek I n jest liczba parzysta Wówczas musi być x−1>0 ale znaleziona wartość x daje

	2
x−1=		}
	(2+ε√3)n−1

Aby był spełniony warunek x−1>0 należy wziąć ε=1 Przypadek nr II n jest liczba nieparzysta Liczby x+1 i x−1 musza być jednakowych znakow Wiemy ze gdy wezniemy ε=+1 liczba x−1 będzie dodatnia a wiec również i liczba x+1 będzie dodatnia . Gdy natomiast wezniemy ε=−1 liczba x−1 będzie ujemna ale latwo wykazac (u niego wszystko latwo ) ze wówczas liczba x+1 będzie ujemna . Ostatecznie wzor (2) można napisac w postaci

	(2+εn√5)n+1
x=
	(2+εn√3)n−1

Przy n parzystym jest jedno rozwiązanie a przy nieparzystym dwa

5-latek: czy Tobie tez od dzisiaj z lewej strony w dolnym rogu wlaczaja się reklamy ? Jeśli tak tak jak to dziadostwo wylaczyc ? Jeli nie da rady to zrezygnuje z forum . Nie lubie tego

henrys: cześć 5−latku u mnie żadne reklamy się nie wyświetlają. Niestety nie mam zbiorku z którego korzystasz, bo nie wiem co to za zbiorek. Napisałem rozwiązanie z tego co zamieściłeś dlatego pytałem czy coś takiego masz w odpowiedziach. Co do dyskusji to słaby ze mnie rozmówca Czytałeś co napisałem dla n=2? Według moich obliczeń są dwa rozwiązania bez względu na parzystość n, dokładnie takie jak zamieściłem

5-latek: Zbior zadań jest stary i ma już 60 lat . Raczej już niedostępny Wczoraj już musialem isc spac bo rano miałem do pracy jednak teraz bardziej interesuje mnie jak doszsedles Ty do rozwiązania z 22:21 czt sugerowales soe podpowiedzia Saizou?

henrys: Przypadek I x−1>0 nie musi zachodzić

	x+1
Iloraz		jest zawsze dodatni
	x−1

Wydaje mi się, że pokazałem jak to działa dla n=2. Jedyny warunek to x∊(−∞,−1)u<1,∞) i dla tych rozwiązań jest spełniony

henrys: Nie sugerowałem się jego podpowiedzią

henrys: robiłem dokładnie takie podstawienia jak napisałeś parę godzin temu

5-latek: Witaj witaj Jutro już przeczytam twój post 0:10. najpierw przetrawię to rozwiązanie ze zbioru

henrys: a jednak robiłem trochę inne te podstawienia:

	x+1
u=		(dopiero doczytałem co tam napisałeś)
	x−1

1
	=a
n

różnica niewielka, ale dla n parzystego Twoje podstawienie rzeczywiście sugeruje, że x+1>0

	x+1
dlatego myślę, że podstawienie u=		jest bardziej właściwe.
	x−1

5-latek: Witaj jeszce później się tym zajme . Teraz nie ma glowy do tego .

henrys: pomyślałeś 5−latku? może ktoś zerknie?

prosta: analizuję to rozwiązanie z odpowiedzi i nie widzę uzasadnienia dla założenia: x−1>0

henrys: bo go nie ma...

prosta: hmmm...ale przy założeniu v=ⁿ√x−1 wypadałoby o tym pomyśleć.... ...tylko w początkowym równaniu mamy ⁿ√x²−1...hmmm

prosta: ogólnie..skoro w równaniu występuje ⁿ√x²−1 i uwzględnimy prawą i lewą stronę równania możemy przyjąć za dziedzinę x∊(−∞,−1)∪(1,+∞)

henrys: pewnie, tylko czy warto robić akurat takie podstawienie?

Metis: Cześć 5−latku Pewnie masz złośliwe oprogramowanie, coś Ci się pewnie zainstalowało. Na forum nie ma żadnych reklam, choć dzisiaj pojawiły się małe zmiany na forum: https://matematykaszkolna.pl/regulamin.21.08.15.pdf

henrys:

	x+1
v=		jest mniej konfliktowe
	x−1

prosta:

5-latek: czesc Metis Wlasnie to widziałem

Metis: Teraz komunikaty już znikły

6xdj: Tez to rozwiązanie mnie interesuje

6xdj: Może najpierw według podpowiedzi 5−latka z 17.08 z 17:38 Bo jeśli to równanie zapiszemy inaczej (ⁿ√x+1)²+(ⁿ√x−1)²=4ⁿ√x²−1 jeśli oznaczymy u=ⁿ√x+1 i v=ⁿ√x−1 i ⁿ√x²−1= ⁿ√(x+1)(x−1)= ⁿ√u*v u²+v²=4uv Dlaczego teraz pisza ze liczba u i v nie może być zerem ?

6xdj: bo 0²+0²= 4*0*0 to 0=0 (przecież to prawda

henrys: to nie jest prawda, bo jeśli u=0, to x+1=0 ⇔x=−1,⇒v=ⁿ√−2, 0+(ⁿ√−2)²≠0, pomijając już parzystość n (czyli gdy u=0 to v≠0, a gdy v=0 to u≠0, ale uv=0). Druga sprawa, jeżeli n jest parzyste, to w ogóle nie można tak zapisać tego równania, chyba, że założymy, że x>1, dlatego dają założenie x−1>0 dla n parzystych i dostają tylko jedno rozwiązanie, bez rozpatrzenia x−1<0, bo im to nie pasuje do podstawienia.

6xdj: OK. Dzieki

henrys: ale trudno uwierzyć żeby takie rozwiązanie podali w książce...

6xdj:

5-latek: Jutro się okaze czy wszystko będzie w porządku . Jeśli tak to się tym zajme dalej

Mila: Wyjaśnienia: 1) żadna z liczb u i v nie może być zerem . Jeśli x+1=0⇔x=−1 wtedy mamy sytuację: ⁿ√0+ⁿ√(−1−1)²=4*ⁿ√(1²−1)⇔ ⁿ√4=0 sprzeczność Jeśli x−1=0⇔x=1 Wtedy: ⁿ√(1+1)¹+ⁿ√0=ⁿ√(1−1)⇔ ⁿ√4=0 sprzeczność.

5-latek: dziekuje CI bardzo na razie

Mila: Co jeszcze z tego wyjaśnić, skopiuj frazę.

5-latek: Dobry wieczor Milu

	u
Z równania kwadratowego wyliczyliśmy stosunek		i wyszlo nam ze
	v

u		u
	= 2+√3 lub		= 2−√3
v		v

	n√x+1
Teraz		= 2+√3(obie strony do potęgi n i mamy
	n√x−1

x+1		(2+√3)n+1
	= (2+√3)n z tego mamy x=
x−1		(2+√3)n−1

==============================

	u		(2−√3)n+1
Jeżeli za		wsywawimy 2−√3 to x=
	v		(2−√3)n−1

============================ Teraz przejdźmy do dyskusji jeśli n jest parzyste to x−1 >0 dlaczego ?

5-latek: Czy dlatego z e wtedy prawa strona jest dodatnia zarówno dla

x+1		x+1
	= (2+√3)n a także dla		=(2−√3)n bo (2−√3)n gdy n jest
x−1		x−1

parzyste jest dodatnie / Ale dlaczego przyjmują wtedy ze x+1 jest zawsze dodatnie ?

5-latek: Poprawka Mialo być tak bo (2−√3)ⁿ i 2+√3)ⁿ przy n parzystym jest dodatnie

	2
Teraz x−1 =
	(2±√3)n−1

I teraz żeby x−1>0 to musi wtedy być (2+√3)ⁿ−1 bo licznik mamy dodatni 2>0 i mianownik musi być dodatni a dodatni będzie dla (2+√3)ⁿ−1

Mila:

looomp: dlaczego x−1>0

Mila: Jeżeli n jest parzyste to dla wyrażenia w początkowym równaniu : ⁿ√x²−1 dziedzina: x²−1≥0⇔(x+1)*(x−1) ≥0⇔x≤−1 lub x≥1 ustaliliśmy wcześniej, że x≠1 i x≠−1 stąd x<−1 lub x>1 Jeśli weźmiemy przedział x>1 to obydwa wyrażenia : x−1>0 i x+1>0 ( tak?) Ja rozwiązywałabym równanie tak: ⁿ√(x+1)²+ⁿ√(x−1)²=4ⁿ√(x+1)*(x−1) /: (ⁿ√(x+1)*(x−1)⇔

	(x+1)2		(x−1)2
[		]1n+[		]1n=4⇔
	(x+1)*(x−1)		(x+1)*(x−1)

	(x+1)		(x−1)
[		]1n+[		]1n=4
	(x−1)		(x+1)

Teraz podstawienie:

	(x+1)
[		]1n=u
	(x−1)

	1
u+		=4 /*u
	u

u²−4u+1=0 Dalej otrzymasz :

	(x+1)		(x+1)
[		]1n=2−√3 lub [		]1n=2+√3
	(x−1)		(x−1)

(x+1)		(x+1)
	=(2−√3)n lub		=(2+√3)n
(x−1)		(x−1)

looomp: dzięki

5-latek: Dobrze Milu czyli to x+1>0 wynika z dziedziny Teraz moje rozumowanie ze (2−√3)ⁿ i (2+√3)ⁿ przy n parzystym jest >0 to wobec tego x−1>0 musi być dodatnie jest prawidłowe Tak ? Wtedy mamy jedno rozwiązanie . Teraz zajmijmy się n −niepatrzystym Ciezko mi trochę to zrozumieć dlaczego x+1 i x−1 musza być jednakowych znakow ?

Mila: (x+1)*(x−1)>0 ⇔ x+1>0 i (x−1)>0 lub x+1<0 i x−1<0 Dlaczego jedno rozwiązanie, są (wg mnie) dwa rozwiązania spełniające te warunki. ( Chyba, że czegoś nie zauważam). Sprawdź w wolframie dla konkretnych n.

5-latek: Milu Przepisalem dokładnie podpowiedz do tego zadania ze zbioru . takie rozwiązanie podal prof. Antoni Rusiecki . Ty się sugerowałem pisząc o jednym rozwiązaniu dla n parzystego . Post 20:09 Natomiast jeśli chodzi o n nieparzyste to nie musimy się przejmowc dziedzina . Stad moje pytanie dlaczego x+1 i x−1 musza być jednakowych znakow

	x+1
Jeśli będą jednakowych znakow to stosunek		będzie dodatni
	x−1

Mila: 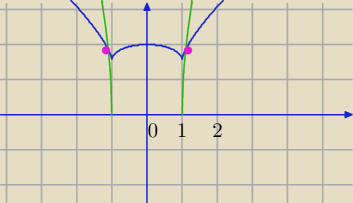√(x+1)²+√(x−1)²=4√x²−1

Mila:

x+1
	ma taki sam znak jak iloczyn (x+1)*(x−1) =x2−1
x−1

W odpowiedzi masz, że dla n parzystego jest jedno rozwiązanie?

5-latek: Tak Milu Mam w odpowiedzi ze jedno rozwiązanie no chyba ze się pomylili a erraty nie mam

Mila: Może czegoś nie uwzględniłam. Będę jeszcze myśleć.

5-latek: Dobrze Milu Wlasnie dlatego tak sobie to tlumaczylem . jeśli nic się nie wymyśli to nie będzie tragedii