proszę o pomoc Depay: rozwiąż nierówności x(x+6) 3</(4x−3)

J: x² + 6x − 4x + 3 < 0 ⇔ x² + 2x + 3 < 0 ... a teraz dasz radę ?

5-latek: Wedlug zapisu wygląda to tak

x(x+6)3<
	zycze powodzdenia
4x−3

Depay: x(x+6) 3 mniejsza równe (4x−3)

5-latek: Witaj J

5-latek: Czy tak ? x(x+6)*3≤4x−3?

J: Cześć ... no to popraw znak w poście: 10:54 na: ≤

J: nie .....( nie widziałem tej 3 )

Depay: x(x+6)≤3(4x−3)

5-latek: tak wlasnie myslalem bo po co bylby ten nawias przy (4x−3) no to teraz wymnazaj nawiasy

Depay: x²+6x≤12x−9

5-latek: Teraz wszystko na lewa strone i przyrownac do zera Zobaczyc czy cos się nie zredukuje Uwaga na znaki przy przenoszseniu

Depay: x²−6x−9=0

J: źle ..

Depay: jak zawsze

mat: ............ x²−6x+9≤0 ⇔(x−3)²≤0 ⇒ x=3

J: x² − 6x + 9 ≤ 0

Depay: x²−6+9=0

Depay: delta teraz?

5-latek: Nie (−9) tylko +9 Po drugie to jest nierownosc a nie równanie wiec ≤0 a nie (=0)

Depay: delta = 0 więc x1=3

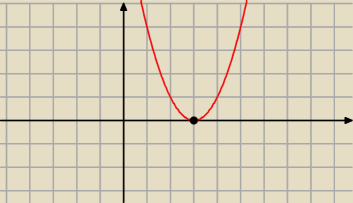
5-latek: Skoro nie zawazyles/as wzoru skroconego mnożenia x²−6x+9= (x−3)² to dobrze Teraz jeśli narysujemy wykres y= x²−6x+9 to dla jakich x_ow ta funkcja będzie przybierala wartości <0 i rowna 0 ?

5-latek: Mialo być to dobrze x_1,2=3

Depay: nwm

5-latek: To odpowiedz mi na pytanie Na której osi OX czy OY odzczytujemy wartości funkcji ? (zresztą każdej funkcji

J: " wartości < 0 i równe 0" ?

mat: przerost formy nad treścią

Depay: OY

Depay: od − nieskończoność do 3 i od 3 do + nieskończoność

5-latek: J napisałem rowna 0 (post 11:28 mat OK tylko tylko ze nikt mu /jej dokładnie nie wytłumaczy żeby zrozumial/la

J: Czy Ty masz pojęcie, co to jest wykres funkcji ?

5-latek: Dobrze Odczytujemy na osi OY To teraz zobacz dla x=3 ile wynosi wartość tej funkcji ?

Depay: 0

J: małolat ... nie może być: wartości mniejsze od zero i równe zero .... lub

5-latek: Tak masz racje . Ma być lub rowna 0 .

5-latek: Teraz czy znajdziesz takie x_sy żeby wartości funkcji były <0?

5-latek: No co tak długo się zastanawiasz ?

5-latek: Skoro nie widzisz na wykresie to może tak Mamy y=(x−3)² dla x=3 y= (3−3)²=0²=0 wezmy np. x=4 to y= (4−3)² = 1²=1>0 wezmy x=6 to y= (6−3)²=3²=9>0 Zauwaz ze dla x>3 y>0 Wezmy teraz x<3 np. x=2 y=(2−3)²=(−1)²=1>0 x=−1 to y= (−1−3)²= (−4)²=16>0 Zauwaz ze dla x<3 y>0 Wniosek . Nie znajdziemy takich x_ow żeby y<0 Teraz (x−3)²≤0 jest spełnione tylko dla x=3 . Koniec

Eta: "małolatku" co Ty wypisujesz? po co? (x−3)²≤0 spełniona tylko dla x= 3 kwadrat liczby nie może być ujemny jedynie może być równy zero zatem x−3=0 ⇒ x=3 koniec

Eta: To wiedzą już Twoi koledzy z przedszkola

pigor: ..., a więc podsumowując np. tak : x(x+6) ≤ 3(4x−3) ⇔ x²+6x−12x+9 ≤ 0 ⇔ x²−2x*3+3² ≤ 0 ⇔ ⇔ (x−3)² ≤ 0 ⇔ |x−3| ≤ 0 ⇔ x−3= 0 ⇔ x= 3 ⇔ x∊{3}. ...

5-latek: Dzien dobry Eta Ja to wiem ale czy on/ona to wie ? czy miał/la wytlumaczone to porządnie ? Być może ? Tylko z tego względu to napisałem Dzisiaj już tak u mnie nie grzeje

Eta: Jak nie umie prostej nierówności kwadratowej, to ......tym bardziej modułów

pigor: ..., dla kogo prosta to prosta, skąd ta pewność, a może drzemie w Nim ... ,a gdzie jak nie tu (jak nie potrafi gdzie indziej), ma okazję "zobaczyć" różnorodność (piękno) rozwiązań (matmy) , a więc np.to : (x−3)² ≤ 0, to pierwiastkując obustronnie ⇔ √(x−3)² ≤ √0 ⇔ |x−3| ≤ 0 ⇔ ⇔ |x−3|= 0 lub |x−3|< 0 ⇔ x−3= 0 lub x∊∅ ⇔ x=3 i tyle, ... −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−− a więc jak nie On, to może kto inny zechce to wszystko zrozumieć i następnym razem w podobnych okolicznościach mocno ...skracać

Eta: