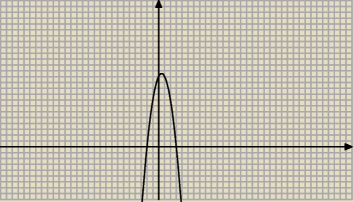
 a) dobrze
b)y∊(−∞;12,5>
Ogólnie to jest dla a>0, y∊<q;+∞) dla a<0, y∊(−∞;q>
a) dobrze
b)y∊(−∞;12,5>
Ogólnie to jest dla a>0, y∊<q;+∞) dla a<0, y∊(−∞;q>
| 1 | ||
funkcja rośnie dla x∊(−∞; | > | |
| 2 |
| 1 | ||
funkcja maleje dla x∊< | ;+∞) | |
| 2 |
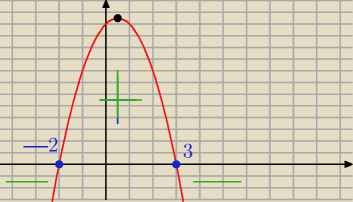 a) dobrze
b) Zbior wartości odcztytujemy na osi OY i
jeśli a>0 to ZWf= <q,∞)
==========================
jeśli a<0 to ZWf= (−∞,q>
==========================
Przedzialy monotoniczności
Patrz na wykres
Zobacz ze dla x∊(−∞ p> funkcja ta rosnie a dla x∊<p ,∞) funkcja ta maleje
Z tego wynika ze ta funkcja nie jest momotoniczna(tzn nie jest scisle rosnaca lub malejaca )
natomiast jest przedziałami monotoniczna
Argumenty dla których funkcja przyjmuje wartości niedodatnie
Wartosci niedodatnie sa to wartości mniejsze bądź rowne zero
Wiec należy rozwiazac nierownosc
Z wykresu widzisz ze funkcja ta przyjnuje wartości dodatnie dla x∊(−2,3) natomiast wartości
niedodatnie dla x∊(−∞,−2>U<3,∞)
Jeśli nie masz wykresu to należy rozwiazac nierownosc
−2x2+2x+12≤0
a) dobrze
b) Zbior wartości odcztytujemy na osi OY i
jeśli a>0 to ZWf= <q,∞)
==========================
jeśli a<0 to ZWf= (−∞,q>
==========================
Przedzialy monotoniczności
Patrz na wykres
Zobacz ze dla x∊(−∞ p> funkcja ta rosnie a dla x∊<p ,∞) funkcja ta maleje
Z tego wynika ze ta funkcja nie jest momotoniczna(tzn nie jest scisle rosnaca lub malejaca )
natomiast jest przedziałami monotoniczna
Argumenty dla których funkcja przyjmuje wartości niedodatnie
Wartosci niedodatnie sa to wartości mniejsze bądź rowne zero
Wiec należy rozwiazac nierownosc
Z wykresu widzisz ze funkcja ta przyjnuje wartości dodatnie dla x∊(−2,3) natomiast wartości
niedodatnie dla x∊(−∞,−2>U<3,∞)
Jeśli nie masz wykresu to należy rozwiazac nierownosc
−2x2+2x+12≤0