Prosze o wytłumaczenie Nowy: Jak rozwiązuje sie tego typu zadanie Dla jakich wartosci x okreslona jest liczba m ? m= log(x−4) m=log₂(x²−4) m=log₃(x²−5x+6)

Eta: 1/ x−4>0 ⇒.... 2/x²−4>0 ⇒(x−2)(x+2) >0 ⇒ x∊..... 3/ x²−5x+6>0 ⇒(x−2)(x−3)>0 ⇒x∊ ...

5-latek: Liczby logarytmowane >0

Nowy: czyli np w 1) x∊(4,∞) a to o to chodziło dzieki nie bardzo rozumiałem dzieki Eta,5−latek

Nowy: Czy ta podstawa logarytmu ma jakis wpływ ? 3) np x∊ (−∞3) lub x∊(2,∞) Nie brałem pod uwagę tą podstawe logarytmu

5-latek: tutaj akuratnie podstawa nie ma wpływu gdyż podstawe ma sz nierowna 1 i wieksza od zera . 3) Jest rozwiaanie zapisane zle Powinno być tak x∊(−∞,2)U(3∞)

Nowy: a tu złe przepisałem odp do 3 ale zeszycie mialem dobrze . A w jakim wypadku ta podstawa ma znaczenie w tego typu zadaniu ?

Eta: log_ab , b>0 i a>0 i a≠1 log₂x to tylko x>0 bo 2>0 i 2≠1 log_x5 to x>0 i x≠1 log_x−2 (x+1) to x+1>0 i x−2>0 i x−2≠1 ⇒ x∊(2,∞)\{3}

Nowy: log_x−2 (x+1) x∊(1,∞)\ {2,3} x−2>0 x−2≠1 x−1>0 x>2 x≠3 x>1 A nie tak ? Dzieki za wyjasnienia

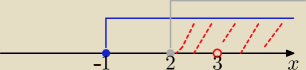
Eta: x>2 i x> −1 i x≠ 3 ⇒ x∊(2,∞) \ {3}

Nowy: Ok juz to widze , jeszcze raz dzieki

Eta: Oczywiście niebieskie i szare kółeczko na rys ma być puste (sorry za chochlika)

Nowy: wiem