Dowód Przemysław: Danych jest 6 niespółliniowych punktów na płaszczyźnie. Wszystkie łączymy odcinkami koloru czerwonego lub niebieskiego. Udowodnij, że zawsze znajdzie się trójkąt jednego koloru. Proszę o pomoc

zombi: https://pl.wikipedia.org/wiki/Twierdzenie_Ramseya to ci się może przydać. Kliknij w przykład. Na kombinatoryce robiliśmy to zadanie, ale teraz nie pamiętam jak to dobrze opowiedzieć.

Przemysław: Dziękuję Tam w przykładzie jest dokładnie teza z tego zadania Będę musiał to ogarnąć.

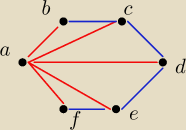
zombi: Chodzi o wybranie możliwie najgorszego przypadku i pokazanie, że i tak wyjdzie co ma wyjść. Tzn. mamy 6 nwspl. punktów (a,b,c,d,e,f). Wybieramy jeden wierzchołek grafu, czyli jeden punkcik. Dajmy na to punkt a. Z niego kolorujemy na czerwono odcinki ab,ac,ad,ae,af. A odcinki bc,cd,de,ef na niebiesko. To nasz możliwie najgorszy wybór (tzn. taki, żeby nie wyszedł jednokolorwy trójkąt). Ale ma być to graf pełny, czyli musimy połączyć wszystkie punkty, ale przy kolorowaniu jakie wybraliśmy, pokolorowanie jakiegokolwiek odcinka będzie równoznaczne z powstaniem jednokolorowego trójkata. Rysunek.

zombi: Coś takiego było u mnie na kombinatoryce, nie wiem na ile poprawne, bo słabo pamiętam.

Przemysław: A jak uzasadnić, że ten wybór jest najgorszy z możliwych? Jeszcze można by spróbować tak: ile jest możliwych kolorowań ile jest wszystkich kolorowań bez trójkątów jednokolorowych i pokazać, że tego drugiego jest mniej niż pierwszego.

Przemysław: Może się mylę, ale wszystkich kolorowań jest chyba 2¹⁵, kolorowań bez trójkątów jest 2¹⁰ prawdopodobieństwo trafienia na graf z trójkątem jednokolorowym − P(A)

	210
(1−P(A)=		=2−5
	215

P(A)=1−2⁻⁵>0 <−− czyli jest niezerowe − są takie grafy

Vax: Oznaczmy te punkty jako A₁, A₂, ..., A₆. Rozważmy wierzchołek A₁, wychodzi z niego 5 krawędzi, więc z zasady szufladkowej Dirichleta pewne 3 są jednego koloru (np czerwonego), niech bso będą to A₁A₂, A₁A₃, A₁A₄ Jeżeli teraz A₂A₃ albo A₃A₄ jest koloru czerwonego, to dostajemy trójkąt o krawędziach jednego koloru. Załóżmy więc, że A₂A₃ oraz A₃A₄ są niebieskie. Ale wówczas jeżeli A₂A₄ jest niebieska, to trójkąt A₂A₃A₄ spełnia tezę, a w przeciwnym wypadku tezę spełnia trójkąt A₁A₂A₄.

Przemysław: Dziękuję bardzo Vax.