czworokąty
onaa: Mam 2 zadania z geometrii do rozwiązania i jedno do sprawdzenia:
1.Z kawałka materiału w kształcie trapezu prostokątnego o podstawach długości 1,2 m i 0,4 m
oraz wysokości 1,5 m wycięto chorągiewkę w kształcie trójkąta równoramiennego,którego podstawą
jest dłuższe ramię trapezu,a jeden z wierzchołków należy do krótszego ramienia trapezu.
a)Wyznacz długości odcinków,na jakie ten wierzchołek podzielił krótsze ramię trapezu.
b)Oblicz długości boków chorągiewki.
Wyniki podaj z dokładnością do 0,01 m.
2.Skwer ma kształt rombu o boku mającym długość 65 m. Wzdłuż przekątnych rombu biegną alejki
spacerowe,z których jedna jest o 70 m dłuższa od drugiej. Oblicz długość tych alejek.
3.Różnica miar kątów przeciwległych trapezu równoramiennego wynosi 20º. Oblicz miary kątów
trapezu.
α−kąt mniejszy
β−kąt większy
α+β=180º
β−α=20º
2β=200
β=100º
α=80º
miary kątów trapezu to: 80º,80º,100º,100º
czy to jest poprawnie rozwiązane?
5 sie 16:51
Eta:
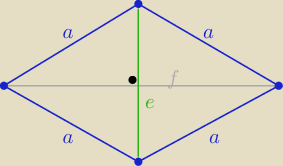
a=65 m
Długość alejek : e i f = e+70 i e,f>0
z tw. Pitagorasa :
| | e | | f | |
( |
| )2+( |
| )2=a2 ⇒ e2+f2=4a2 |
| | 2 | | 2 | |
e
2+(e+70)
2=4*65
2
rozwiąż to równanie .....
otrzymasz odp: e= 50 m i f=120 m
5 sie 22:09
onnn: sprawdzone
6 sie 16:19
J:
Zad 1) .. niewykonalne ... ( sprawdź treść)
6 sie 17:05
J:
6 sie 17:07
onaa: Tak jest w treści.
6 sie 17:14
J:
no to nie da się wyciąć takiej chorągiewki
6 sie 17:16
onaa: Taką mam podać odpowiedź

6 sie 17:18
J:
sorry ... da się

6 sie 17:20
J:
6 sie 17:20
J:
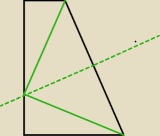
6 sie 17:21
J:
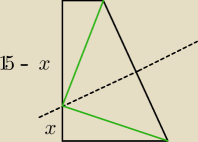
mamy.. (1,5 − x)
2 + (0,4)
2 = x
2 + (1,2)
2 ... i z tego wyliczamy: x
dalej już prosto ...
6 sie 17:37
 a=65 m
Długość alejek : e i f = e+70 i e,f>0
z tw. Pitagorasa :
a=65 m
Długość alejek : e i f = e+70 i e,f>0
z tw. Pitagorasa :



 mamy.. (1,5 − x)2 + (0,4)2 = x2 + (1,2)2 ... i z tego wyliczamy: x
dalej już prosto ...
mamy.. (1,5 − x)2 + (0,4)2 = x2 + (1,2)2 ... i z tego wyliczamy: x
dalej już prosto ...