Geometria XXX: W romb którego bok ma długość 5 cm a kąt ostry 60°, wpisano okrąg. Oblicz pole czworokąta otrzymanego przez połączenie kolejnych punktów styczności tego okręgu z bokami rombu. Do tego już doszedłem − Obliczam pole rombu P=5*5*sin 60°=12,5√3 − Obliczam wysokość rombu H=2,5√3

	1
− Obliczam promień okręgu wpisanego w rombu r=		H=1,25√3
	2

− Obliczam długość krótszej przekątnej d₁=5 − Punkty styczności dzielą bok rombu na odcinki długości x, 5−x no i ewentualnie to np. 5−x

	325
można policzyć z Pitagorasa (5−x)2=		ale dalej wychodzą kosmiczne wyniki
	16

XXX: Wyszło

	25
(5−x)2=		i dalej obliczenia już ida ok
	16

J:

	a		d2
Pole prostokata = a*b oraz:		=		,
	b		d1

gdzie: d₁ − krótsza przekątna, d₂ − dłuższa przekatna

XXX: skad ten stosunek

J: popatrz tutaj: http://matma4u.pl/topic/40617-okrag-wpisany-w-romb/

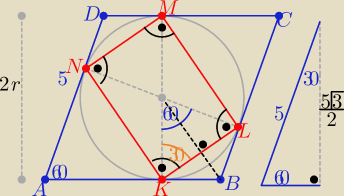Eta: Można też tak:

	5√3
2r=
	2

Czworokąt KLMN jest prostokątem o przekątnych długości 2r i kącie między nimi 60^o

	1		1		5√3		√3		75√3
P(KLMN)=		*2r*2r*sin60o =		*(		)2*		=		[j2]
	2		2		2		2		16

i to wszystko