ciągi onaa:

	2
Dany jest ciąg o wyrazie ogólnym an=4 −
	n

a) Wypisz sześć początkowych wyrazów ciągu b) Narysuj wykres tego ciągu c) Czy ciąg jest ciągiem rosnącym? Odpowiedź uzasadnij

	15
d) Zbadaj,czy istnieje taki wyraz ciągu,który jest równy
	4

J: a) podstawiaj i licz b) ołowek

	an+1
c) znak:
	an

	2		15
d) 4 −		=		.. i n ∊ N
	n		4

onaa: co mam podstawić do czego?

J: n = 1

	2
a1 = 4 −		= 4 − 2 = 2 ... itd.
	1

onaa: czyli a₁=2

	2
a2= 4−		=4−1=3
	2

czyli a₂=3 ?

J: tak .. licz pozostałe

onaa:

	2
a3=
	3

	1
a4=1
	4

	1
a5=1
	5

	1
a6=1
	6

tak? czy źle?

J:

	2
a3 = 4 −		= ...?
	3

J:

	2
a4 = 4 −		= ...?
	4

5-latek: Zle . Tak naprawdę to jest szkola podstawowa a nie liceum

onaa:

	1
a3=3
	3

	2
a4=3
	4

	3
a5=3
	5

	4
a6=3		?
	6

J: tak .. teraz wykres

onaa: jak go narysować?

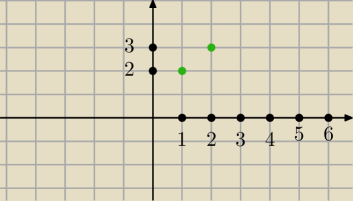
J: a₁ → 2 a₂ → 3 ... itd.

onaa: rozumiem,dziękuję natomiast,co do punktu c) będzie,że ciąg jest ciągiem rosnącym,tak?

J:

	an+1
tak .. ale trzeba to pokazać.. albo: an+1 − an > 0 lub		> 0
	an

5-latek: Wolalbym widzieć obliczenia

onaa:

	2		2
4−		+1−4−		>0 ?
	n		n

J:

	2   4 −   n+1
łatwiej skorzystać z drugiego warunku..		= ...
	2   4 −   n

J: ... i pokazać,że to wyrażenie dla dowolnego n jest > 0

J:

	(4n+2)*n
dojdziesz do postaci:		... i łatwo wykazać,że to jest zawsze dodatnie
	(n+1)*(4n−2)

onaa: nie umiem

J: u góry i u dołu sprowadź do wspólnego mianownika , potem mnożenie licznika przez odwrotnośc mianownika i dostaniesz postac,którą podałem...

onaa: u góry sprowadzamy do n+1 a u dołu do n?

J: tak

J:

	4(n+1) − 2		4n+2
licznik: =		=
	n+1		n+1

	4n−2
mianownik: =
	n

J: teraz: (4n+2) > 0 , n > 0 , (n+1) >0 ,(4n − 2) > 0 ... a więc cały iloraz jest dodatni ..cnw.

Mat3:

an+1
	>1 przy ciągu rosnącym o wyrazach dodatnich ...tak ?
an

J: tak ... już jestem trochę zmęczony ...

J: trzeba zatem pokazać,że : (4n+2)*n > (n+1)(4n−2) ... a to już banał..

onaa: okeej,a to d) jeszcze tylko

J: dochodzimy do postaci: 2n > 2n − 2 ⇔ 0 > − 2

J: d) pomnóż obustronnie przez : 4n

J: 16n − 8 = 15n ⇔ n = 8 ( ósmy wyraz )

onaa: n=8 ?

J:

onaa: dziękuję