rozwiąż nierówność
teusz: x ≠ 0
przenosiłem 2 na lewą stronę i doszedłem do:
mogę teraz pomnożyć obustronnie razy "x" ?
undefined
2 sie 15:29
J:
nie .... ⇔ (1−2x)*x > 0
2 sie 15:30
J:
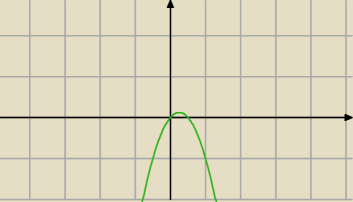
2 sie 15:32
2 sie 15:33
J:
tak
2 sie 15:34
Saizou :
nie możesz, bo nie wiesz jakiego znaku jest x
−gdyby x>0 to mamy
1−2x>0
−gdyby x<0 to mamy
1−2x<0
| | 1 | |
zatem ostatecznie x∊(0, |
| ) |
| | 2 | |
Żeby tego nie rozdrabniać na przypadki to stosuję się zamianę ilorazu na iloczyn, w praktyce
jest to mnożenie przez wyrażenie, które ma stały znak, a takowym jest kwadrat mianownika czyli
w tym przypadku x
2, tzn.
| 1−2x | |
| >0 /x2 (bo x2>0 zawsze) |
| x | |
x(1−2x)>0 i otrzymujemy nierówność wielomianową
2 sie 15:35
teusz: dziękuje

2 sie 15:36
J:
jeśli iloraz dwóch liczb jest dodatni , to ich iloczyn też musi być dodatni ( bo obydwie
liczby muszą mieć ten sam znak)
2 sie 15:37

