logarytmy prosta: : : : maturka czerwiec'2015 : : : Zad.8

	6a
Niech a=log122. Wykaż, że log664=		.
	1−a

J: i gdzie jest problem ?

	6
log664 = U{log264{log26 =
	log26

	log22		1−a
a =		⇔ log26 =
	1 + log26		a

	6		6a
podstawiamy:		=
	1−a   a		1−a

henrys:

	log62		log62
a=log122=		=		=
	log612		log6(2*6)

	log62		log62
=		=
	log62+log66		log62+1

log₆2=t

	t
a=
	t+1

a(t+1)=t at+a−t=0 t(a−1)=−a/:(a−1)≠0

	a
t=
	1−a

	6a
log664=log626=6log62=6t=
	1−a

z1o: log₆64 = 6log₆2 =

	6log122
=		=
	log126

	6log122
=		=
	log12(12/2)

	6log122
=
	1−log122

J:

	log264		6
miało być: log664 =		=
	log26		log26

Mila: Zamień na logarytmy przy podstawie 2.

J: Witaj Mila ... widzę,że preferujemy tą samą metodę

prosta: dziękuje, nie ma większego problemu.... chodzi o poszukiwanie względnie prostego sposobu rozwiązania a może tak: a=log₁₂2 ⇒ 6a=log₁₂64 i 1−a=log₁₂6

	log1264
stąd:		=log664
	log126

J: Twoim sposobem idziemy od TEZY do ZAŁOŻENIA

Mila: Witam i pozdrawiam

J: Również pozdrawiam..

prosta: wykorzystuję założenie, przekształcam i otrzymuję tezę ...nie mogłabym aż tak się pomylić...mi to się nie zdarza ... .myślę pozytywnie, to podstawa

J: nie będę się sprzeczał...

prosta: teza jest równością.....wychodzę od prawej strony i otrzymuję lewą ...

Eta: Hej prosta Daj linka do tego arkusza ( podstawa i rozszerzenie)

prosta: ok http://zphustolarz.nazwa.pl/szkolamatematyki/arkusze_maturalne.html

prosta: podstawa: http://zphustolarz.nazwa.pl/szkolamatematyki/Arkusze/Maturalne/p.p/CKE%20Egzamin%20maturalny%202015%20Czerwiec%20p.p.pdf rozszerzenie: http://zphustolarz.nazwa.pl/szkolamatematyki/Arkusze/Maturalne/p.r/CKE%20Egzamin%20maturalny%202015%20Czerwiec%20p.r.pdf wygląda na oryginał

Eta: Baaaaaaaardzo dziękuję

prosta:

Asmander:

	m2+m−6
Funkcja f jest określona wzorem f(x)=		x2 −(m−2)x+m−5 dla każdej liczby
	m−5

rzeczywistej x . Wyznacz całkowite wartości parmetru m, dla których funkcja f przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.

m2+m−6
	<0
m−5

Δ>0 x₁x₂>0 mógłby to ktoś jakoś rozjaśnić

Asmander: sprawdziłem w internetach mam dobrze . nie potrzebny post. 10:16

Kacper:

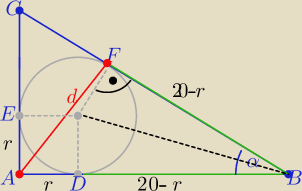
Eta: Matura czerwiec 2015 (rozszerzenie : zad11

	15+20−25
|CB|=25 , r=		= 5 , |BF|=20−r= 15
	2

	20		4
cosα=		=
	25		5

z tw. kosinusów w trójkącie ABF:

	4
d2= 202+152−2*20*15*		⇒ d= √145
	5

Eta: Kto rozwiąże zad12

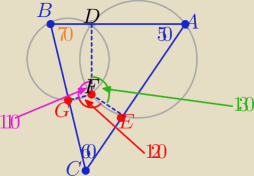Eta: zad.9 Na czworokącie CEFG można opisać okrąg c.n.u bo................ komentarze zostawiam zainteresowanym ... .

pigor: ..., jeśli |CP|=x=?, pole ΔASD=s, pole ΔCSP=p, to z warunków zadania mam np. układ równań :

s−p		p		a−x		2s−p
	=		i		=		⇔
s		2s		x		2s+p

	a		2s−p		a		2p
⇔ 2s−2p= p i		−1=		⇔ 2s= 3p i		−1=		⇒
	x		2s+p		x		4p

	a		3
⇒		=		⇔ 3x = 2a ⇔ x= 23a . c.n.w. ...
	x		2

Benny: Jakoś nie ogarniam tego rozwiązania

Eta: 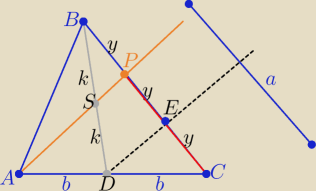zad12 Inny sposób Wykonać rysunek ( zgodnie z treścią zadania dorysować z punktu D równoległą do AP i dwa razy z Talesa : 1/ w trójkącie DBE 2/ w trójkącie ACP

	2
wniosek : |CP|=		a
	3

pigor: ... , ... moje równania są z warunków zadania, że pola ΔSAB= ΔSBC= ΔSCD= ΔSDA są równe, bo parami maja jednakowe podstawy albo wysokości i stąd 1sze równanie to równość stosunków par ΔΔ o jednakowych wysokościach opartych na jednakowych podstawach zaś 2−gie równanie to stosunek pól ΔΔ BSP i PSC "przyległych" do BC o jednakowych wysokościach równy stosunkowi ich podstaw długości a−x i x odpowiednio. ...

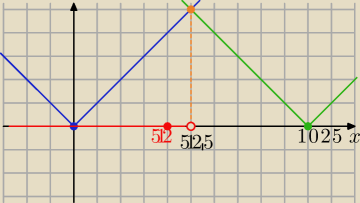
Eta: Zad6 graficznie odp: x= 512 do zakodowania

pigor: ..., analitycznie np. tak : |x|< |x−1025| ⇔ |x|²< |x−1025|² ⇔ x²−(x−1025)²< 0 ⇔ ⇔ (x−x+1025)(x+x−1025)< 0 ⇔ 2x−1025< 0 ⇔ x< 512,5 ⇒ ⇒ x= 512 − szukana największa liczba całkowita. ...

Ania: Kto mi wytłumaczy zad. 12 rozwiązane wg pigora? Nie mogę zrozumieć

kubuspuchatek: pigor mozesz napisac z których doklanie trojkatow sa te rownosci z polami ?

kubuspuchatek: ktos cos ?

zyd: dobra skad s−p/s=p/2s

0: 02_{2√√√α√β√γ√δπΔΩ∞≤≥∊⊂∫←→√⇒⇔∑≈≠Φεθ√λμξρςσφωηϰ√ϱ∀∃∄∅∉∍∌√∏∏⊂⊄⊆√⊃⊅⊇ ≡∟√∠∡√∥∬∭∮∼√⊥⋀⋁∩∪√∧∨¬±ℂ℃℉ℕℙℚℛℤℯ↑↓↔↕↖↗↘↙△□▭▯▱◯⬠⬡♀♂♠♣♥♦}

[object HTMLElement]: [object HTMLElement]2_{2√√√α√β√γ√δπΔΩ∞≤≥∊⊂∫←→√⇒⇔∑≈≠Φεθ√λμξρςσφωηϰ√ϱ ∀∃∄∅∉∍∌√∏∏⊂⊄⊆√⊃⊅⊇≡∟√∠∡√∥∬∭∮∼√⊥⋀⋁∩∪√∧∨¬±ℂ℃℉ℕℙℚℛℤℯ↑↓↔↕↖↗↘↙△□▭▯▱◯⬠⬡♀♂♠♣♥♦}

[object HTMLElement]: <b style="color: red">NIGGER</b>

Drwalin matematyczny: O co chodzi wyżej