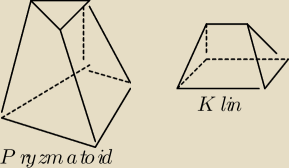
Pryzmatoid
AS:
Czy wiesz,że? (ukłon dla Ety,dzi)
Pryzmatoid
jest to bryła ograniczona dwoma równoległymi wielokątami
(niekoniecznie przystającymi) o ścianach bocznych będących
trójkątami,równoległobokami bądź trapezami.
Objętość takiej bryły wyraża się wzorem
V = h/6*(D + 4*M + d) gdzie
h − wysokość , D,d − pola podstaw,M − pole środkowego przekroju.
Przypadki szczególne
Graniastosłup
Pd = Pg = M = D; V = h/6*(D + 4*D + D) = h/6*6*D = D*h
Ostrosłup
Pd = D , M = D/4 , Pg = 0;
V = h/6*(D + 4*1/4*D + 0) = h/6*(2*D) = 1/3*D*h
Ostrosłup ścięty
Pd = D, Pg = d ,
√M = 1/2*(
√D +
√d) => M = 1/4*(D + 2*
√D*d + d)
V = h/6*(D + 4*1/4*(D + 2*
√D*d + d) + d) = h/3*(D +
√D*d + d)
Walec − jak graniastosłup
Pd = Pg = M = π*R
2 , V = π*R
2*h
Stożek
Pd = π*R
2 , M = 1/4*π*R
2 , Pg = 0 ; V = h/6*(π*R
2 + 4*1/4*π*R
2 + 0)
V = 1/3*π*R
2*h
Stożek ścięty − analogicznie do ostrosłupa ściętego
Pd = π*R
2 , M = π/4*(R
2 + R*r + r
2) , Pg = π*r
2
V = π*h/3*(R
2 + R*r + r
2)
Kula
Pd = 0 , M = π*R
2 , Pg = 0 , h = 2*R ;
V = 2*R/6*(0 + 4*π*R*2 + 0) = 4/3*π*R
3
Klin − podstawa prostokątna o wymiarach a,b krawedź górna c || a
Pd = a*b , Pg = 0 , M = (a + c)/2*b/2 ; V = h/6*(a*b + 4*(a + c)/2*b/2 + 0)
V = 1/6*b*h*(2*a + c)
Pryzma (klin ścięty)
Dolna podstawa prostokątem o wymiarach a1,b1,górna podstawa prostokątem
o wymiarach a2,b2
Pd = a1*b1 , Pg = a2*b2 , M = (a1 + a2)/2*(b1 + b2)/2
V = h/6*(a1*b1 + 4*(a1 + a2)/2*(b1 + b2)/2 + a2*b2)
V = h/6*(a1*b1 + (a1 + a2)*(b1 + b2) + a2*b2)
lub po dalszych przekształceniach
V = h/6*[(2*a1 + a2)*b1 + (a1 + 2*a2)*b2]
Wzory przybliżone
Beczka − R − promień dna,Rs − promień w środku wysokości
Pg = Pd = π*R
2 , M = π*Rs
2
V = h/6*(π*R
2 + 4*π*Rs
2 + π*R
2) = π*h/3*(R
2 + 2*Rs
2)
Butla
Pd = M = π*R
2 , Pg = π*r
2
V = h/6(π*R
2 + 4*π*R
2 + π*r
2) = π*h/6*(5*R
2 + r
2)
Pozdrawiam ASiora 
