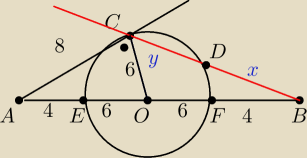
t Andrzej Świnoga: Bez twierdzenia Kosinusów oki Środkiem O odcinka AB o długości 20 cm jest środek okręgu o promieniu 6 cm. Przez punkt A poprowadzono styczną do okręgu w punkcie C. Odcinek CB przecina okrąg w punkcie D. Oblicz CD i DB. Jedyne co mi się udaje zrobić to z tw. o stycznej i siecznej x * (x+y) = 4*16 Umiem to zrobić z Tw.kosinusów ale nie o to chodzi w zadaniu z 1 Liceum przed Trygonometrią

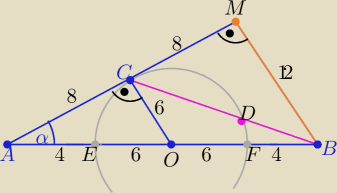nocek: Prowadzimy odcinek BM ⊥AC Trójkąty AOC i ABM są podobne w skali k=2 to (dane na rys) Z tw. Pitagorasa w ΔBCM : |BC|=√12²+8²= ....= 4√13 Z tw. o siecznych

	16√13
|BE|*|BF|=|BC|*|BD| ⇒|BD|=..........=		to |CD|=|BC|−|BD|=............
	13

Kacper:

5-latek: Czesc Kacper Eta nie poszla na brydza