planimetria [c[zmora maturzystów]] Eta: Zadanko dla chętnych W czworokącie wypukłym ABCD na bokach AB i AD obrano odpowiednio punkty M i N tak,że czworokąt AMND jest równoległobokiem. Odcinki DM i BN przecinają się w punkcie K Wykaż,że pola czworokątów AMKN i BCDK są równe.

Mila: O, widzę Etę opaloną.

Eta: Hej Na razie wyłączam komputer bo idzie straszliwa burza

Mila: U mnie już była, jest teraz bardzo miła aura.

Eta: Ufff.... jak fajnie , wreszcie chłodzik

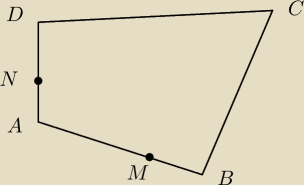
Saizou : i jak tu wyznaczyć czworokąt AMND ?

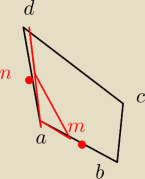
Hugo: jak to narysowac?

Metis: Eta mieszkamy zatem blisko siebie, bo u mnie właśnie po burzy

Janek191: U mnie się zaczęła

Metis: Południowy wschód Polski ?

Hugo: burza ma zasięg około 40km

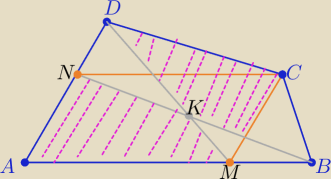
Eta: Sorry Saizou muszę zmienić okulary Poprawka : czworokąt AMCN jest równoległobokiem

Kacper:

Eta: @Kacper masz "chrapkę" na to zadanko?

Saizou : Mnie się wydaje że Kacper kiedyś robił podobne zdanko

Kacper: Oczywiście mam, tylko dzisiaj żniwa i trochę zmęczony jestem A pewnie bez kartki się nie obejdzie

Eta: Kacper niech odpoczywa Łap zadanie Saizou

Saizou : na razie zastanawiam się co jest złego w wektorach zawsze powtarzałem że to zło wcielona

Kacper: Popatrzyłem na zadanie i stwierdzam, że czworokąty z rysunku 19.09 nie mają tych samych pól

Kacper: Jak doczytałem treść, to widzę że rysunek jest zły

Kacper: Zadanie proste. Ja zrobiłem

Eta: Jasne nie dorysowałam fioletu w czworokącie BCDK

prosta: hmm, nie mam pomysła

Eta: Nie wierzę? łatwe

prosta: tak to jest gdy za dużo pomysłów na raz w głowie

Eta: Podpowiedź: dorysuj przekątną AC równoległoboku i wskaż trójkąty o równych polach ........................

Kacper: To ja zapewne na około trochę, ale pierwsza myśl to wykorzystać równoległobok Wrzucić rozwiązanie?

prosta: 1. Jak poprowadzę przekątną AC to widzę trapez o poziomych równoległych podstawach i przecinających się przekątnych: trójkąt po lewej ma takie samo pole jak trójkąt po prawej 2. Po długim przyglądaniu się widzę też drugi trapez z przecinającymi się przekątnymi: tam równe pola mają trójkąty górny i dolny 3. Z równości pól tych trójkątów(powstałych przez cięcie trapezu przekątnymi, zawierających ramiona trapezu) powinna już chyba wyjść równość pól Poczekam na rozwiązanie Kacpra

Eta: Witam prosta dokładnie tak

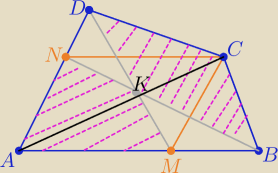
Eta: Z warunków zadania mamy wykazać ,że P(AMKN)=P(BCDK) Z własności równoległoboku P(ABN)=P(ABC) i P(MCD)=P(MCA) P(ABC)=P(MCA)+P(BMC) P(AMKN)+P(BMK)=P(ABN)=P(ABC)=P(AMC)+P(BMC)=P(MCD)+P(BMC)= P(BCDK)+P(BMC) zatem : P(AMKN)+P(BMK)=P(BCDK)+P(BMC) ⇒ P(AMKN)=P(BCDK) c.n.u

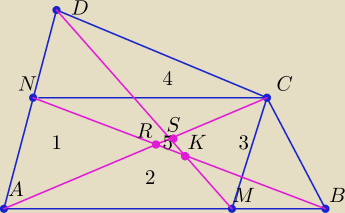
prosta: w trapezie ABCN: P₁=P₅+P₃ w trapezie AMCD: P₄=P₅+P₂ po odjęciu stronami otrzymujemy: P₁−P₄=P₃−P₂ stąd: P₁+P₂=P₃+P₄ P(AMKN)=P(BCDK)

Eta: Też ładnie

prosta:

Mila: Prosta to piękne rozwiązanie.

Eta: Baaardzo piękne !

Eta: Dla chętnych zad2/ Oblicz pole trapezu ,którego przekątne mają długości 15 i 20 a wysokość ma długość 12

Benny: Czy wynik to 150?

Eta: 150 lub 42

Benny: No właśnie coś się zastanawiałem, że za szybko poszło

Benny: No nadal nie wiem jak wyjdzie z tego 42

Eta:

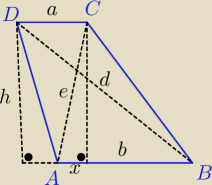
Benny: d=20, e=15, h=12 e²=h²+x² x=9 d²=h²+(a+b)² a+b=16

	a+b+x
P=		*h
	2

	25*12
P=
	2

P=150 No i jak to 42?

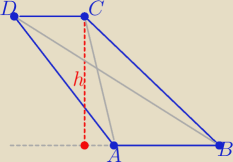
Eta: Na rys. rozważyłeś przypadek gdy spodek wysokości leży na boku AB wtedy pole P=150 rozważ przypadek gdy spodek wysokości leży na przedłużeniu podstawy AB ( poza trapezem)

Benny: Och no tak, wtedy suma podstaw to 7 i dostajemy P=42

Eta: