nierówność z pochodnych
dawidus: Zadanie z pochodnych. Pokaż że 1xex≥14e2x dla x>0.
22 lip 15:35
Janek191:
| | 1 | | 1 | |
|
| ex ≥ |
| e2x , x > 0 ? |
| | x | | 4 | |
22 lip 15:52
dawidus: nie, tak jak jest u mnie napisane
22 lip 15:57
Janek191:
więc
| | −ex | | ex | | 1 | |
f '(x) = |
| + |
| − |
| e2 = 0 ⇔ x = 2 |
| | x2 | | x | | 4 | |
| | ex*x2 − ex*2x | | 1 | | 1 | |
f ''(x) = −[ |
| ] − |
| ex + |
| ex |
| | x4 | | x2 | | x | |
f ''(2) > 0, więc dla x = 2 funkcja f osiąga minimum lokalne
równe y
min = 0 czyli f(x) ≥ 0 dla x > 0
22 lip 16:15
Janek191:
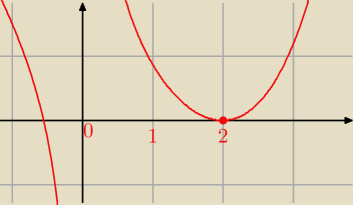
22 lip 16:19
daras: i zrozumiał coś z tego?
22 lip 20:40
Janek191:
Któż to wie ?

23 lip 18:06

