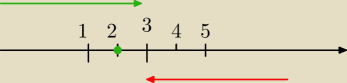
entier bimbam: funkcja entier Mam jeszcze pytanie dotyczące funkcji [x] W książce jest napisane, że określamy funkcję [x] entier x jako największą liczbę całkowitą N spełniającą warunek N≤x Ja to rozumiem w ten sposób. Przy tej funkcji zaokrąglam w dół, bo N≤x. Liczbę x wstawiam sobie w klamrę i szukam takiego N∊C, który jest mniejszy lub równy x Zatem np. [−π]=−4, bo: −π ≈ − 3,14 czyli liczbą mniejszą od (− 3,14) i która zarazem należy do liczb całkowitych jest (−4) Nie do końca wiem, dlaczego gdy mam obliczyć granicę funkcji [x] w punkcie x=3 to lim x→3⁺ [x] =3, bo x∊<3;4) to lim x→3⁻ [x] =2, bo x∊(<2;3) Jeśli x zbiega do 3 od lewej strony, to do tej liczby 3 nie dociera (), więc ostatnią liczbą mniejszą / równą 3, która jest liczbą całkowitą jest liczba 2. Więc tu rozumiem, skąd to lim x→3⁻ [x] =2 Nie wiem, dlaczego jest x∊<3;4) Jeśli x zbiega do 3 od prawej strony, to do tej liczby 3 też nie dociera (), więc jak liczba 3 może być najmniejszą równą spośród tych argumentów, skoro jej w tym przedziale nie powinno być

henrys: Masz definicję ,,określamy funkcję [x] entier x jako największą liczbę całkowitą N spełniającą warunek N≤x"

Mila: Popatrz na wykres; https://matematykaszkolna.pl/strona/979.html

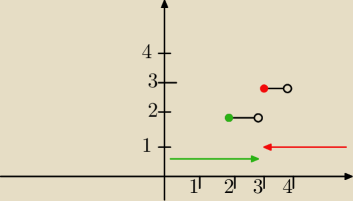
bimbam: czy chodzi o ten fragment wykresu gdy dąży od lewej, to największa liczba całkowita mniejsza od 3 to będzie 2, a w przypadku gdy zbiega od prawej do liczby 3, to największa liczba całkowita to będzie 3

henrys: Tak o ten, wiesz już dlaczego?

bimbam: chyba tak. Dzięki