Oblicz |A∩B|.
Wawrzyniec: Symbol |A| oznacza liczbę elementów skończonego zbioru A. Oblicz |A∩B|, jeżeli zbiory A i B są
podzbiorami przestrzeni U oraz:
a) |U| = 10, |A| = 6, |B'| = 4, |A∪B| = 8,
b) |U| = 10, |A∩B'| = 4, |A'| = 3.
21 lip 19:14
Bogdan:
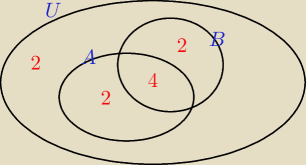
a)
|B| = |U| − |B'| = 10 − 4 = 6
|A∪B| = |A| + |B| − |A∩B| ⇒ 8 = 6 + 6 − |A∩B| ⇒ |A∩B| = 4
21 lip 19:46
henrys: a)
|B|=6,|A|=6, |A∪B|=8 ⇒ |A∩B|=4
21 lip 19:49
Bogdan:
A co henrys proponujesz w punkcie b) ?
21 lip 20:12
=:=:
21 lip 20:34
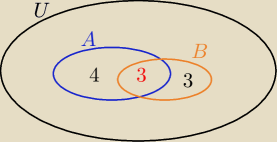
henrys: |A'|=3 ⇒|A|=7,
|B∪B'|=|U| i |B∩B'|=zbiór pusty
|A∩B'| = 4, 4 elementy A należą do B' ⇒ pozostałe 3 elementy A należą do B ⇒ |A∩B|=3
21 lip 21:30
Bogdan:
b)
|A| = |U| − |A'| = 10 − 3 = 7
|A∩B'| = |A| − |A∩B| ⇒ 4 = 7 − |A∩B| ⇒ |A∩B| = 7 − 4 = 3
21 lip 21:37
Wawrzyniec: Dziękuję wszystkim.
22 lip 09:05
 a)
|B| = |U| − |B'| = 10 − 4 = 6
|A∪B| = |A| + |B| − |A∩B| ⇒ 8 = 6 + 6 − |A∩B| ⇒ |A∩B| = 4
a)
|B| = |U| − |B'| = 10 − 4 = 6
|A∪B| = |A| + |B| − |A∩B| ⇒ 8 = 6 + 6 − |A∩B| ⇒ |A∩B| = 4
