x
Michcio: Wyznacz wszystkie wartości parametru m dla których równanie
√ |x−4|−1 = 3−
√3*m ma dwa
rozwiązania dodatnie
Podniosłem stronami do kwadratu i doszedłem do postaci ||x−4|−1|=(3−
√3m)
2
Naszkicowałem wykres funkcji, zauważyłem że musi być spełniona podwójna nierówność
1≤(3−
√3m)
2≤3 czyli 1≤|3−
√3m|≤
√3
Po rozwiązaniu nierówności podwójnej doszedłem do wyniku
| | 2√3 | | 4√3 | |
<√3−1, |
| >∪< |
| ,√3+1> |
| | 3 | | 3 | |
Niestety w odp. na końcu jest tylko ten pierwszy przedział. Dlaczego?
Pytanie dodatkowe:
Czy można narysować wykres funkcji f(x)=
√ |x−4|−1 wychodząc z
√x 
Gdzie jest błąd

20 lip 23:18
Saizou :
podnieść do kwadratu możesz kiedy obydwie strony równania są tego samego znaku, czyli
3−√3m≥0
3≥√3m
m≤√3
20 lip 23:21
Michcio: Ale ogólnie mój sposób był tam dobry

Faktycznie po lewej stronie
√x, po prawej coś, nazwijmy to y
√x=y
y≥0 aby był pierwiastek
Jeszcze przy okazji nie wolno tego rysować w przedziale (3,5) gdzie to co jest pod
pierwiastkiem tzn |x−4|−1 jest na minusie ?
20 lip 23:25
Michcio: Odp. w ksiązce to jednak <√3−1,√3>
20 lip 23:26
henrys: 1) założenia
2) podnosisz do kwadratu liczbę 3−√3m nie wiedząc czy jest dodatnia czy ujemna
3) lepiej rozpisać wartość bezwzględną pod pierwiastkiem i wtedy rysować wykres
20 lip 23:28
Michcio: Gdy x≥4 rysuję
√x−5 czyli od <4,5) będzie pusto

Gdy x<4 rysuję
√−x+3 tutaj dziedzina to −x+3≥0 ⇔x≤3 czyli od (3,4) też niczego nie będzie
Narysować
√x−5 i
√−x+3 umiem
20 lip 23:33
Godzio:
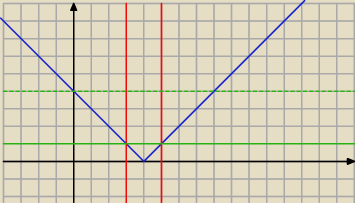
Moja propozycja rozwiązania:
√|x − 4| − 1 = 3 −
√3m
Gdy 3 −
√3m < 0 mamy równanie sprzeczne
Zakładamy zatem, że m ≤
√3.
Określamy dziedzinę dla x,
|x − 4| − 1 ≥ 0 ⇒ |x − 4| ≥ 1 ⇒
x ∊ (−∞, 3> U <5,∞)
Podnosimy równanie do kwadratu
|x − 4| − 1 = 9 − 6
√3m + 3m
2
|x − 4| =
3m2 − 6√3m + 10
Rysuję funkcję
f(x) = |x − 4|
Na zielono narysowałem skrajne przypadki dla funkcji
stałej zależnej od
m
Odczytujemy, że 3m
2 − 6
√3m + 10 musi znajdować się w przedziale <1,4)
No i rozwiązujemy podwójną nierówność
1 ≤ 3m
2 − 6
√3m + 10 < 4
0 ≤ 3m
2 − 6
√3m + 9 i 3m
2 − 6
√3m + 6 < 0
0 ≤ m
2 − 2
√3m + 3 i m
2 − 2
√3m + 2 < 0
0 ≤ (m −
√3)
2 Δ = 4,
√Δ = 2, m
1 =
√3 − 1, m
2 =
√3 + 1
m ∊ R m∊ (
√3 − 1,
√3 + 1)
Pamiętam o naszym założeniu na początku otrzymując odpowiedź:
m ∊ (
√3 − 1,
√3>
=============
21 lip 00:08
21 lip 00:15
Godzio: W książce podałeś, że odp jest obustronnie domknięta, dla
√3 − 1 jednym z pierwiastków jest
0, a nie o to nam chodziło

21 lip 00:18
yyy:
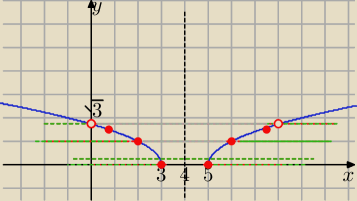 graficznie
graficznie
Rysujesz wykresy :
f(x)= √|x−4|−1 dla x∊ R\ (3, 5)
y=k gdzie k =3−
√3*m
Dwa rozwiązania dodatnie są gdy: 0≤k<
√3 ⇒
3−
√3m≥0 i 3−
√3m<
√3 ⇒ .........
m∊(√3−1, √3>
21 lip 00:20
henrys: |x−4|−1≥0
|x−4|≥1
x−4≥1 lub x−4≤−1
x≥5 lub x≤3
Z tego co napisal
Saizou m≤
√3
podnosisz do kwadratu
|x−4|−1=(3−
√3m)
2
|x−4|=(3−
√3m)
2+1
x−4=(3−
√3m)
2+1 lub x−4=−(3−
√3m)
2−1
x
1=(3−
√3m)
2+5 x
2=−(3−
√3m)
2+3
x
1 ≥5 więc (3−
√3m)
2+5≥5⇒ (3−
√3m)
2)≥0 dla m≤
√3 (bo takie było założenie)
x
2<4 więc 0<−(3−
√3m)
2+3≤3 ⇔(3−
√3m)
2≥0 i 0<−(3−
√3m)
2+3
−(3−
√3m)
2+3>0
−9+6
√3m−3m
2+3>0
3m
3−6
√3m+6<0
Δ=108−72=36
m
1=(6
√3−6)/6=
√3−1
m
2=(6
√3+6)/6=
√3+1
m∊(
√3−1,
√3+1) ale m≤
√3 więc ⇒m∊(
√3−1,
√3)
21 lip 00:21
Michcio: Czyli błąd w odpowiedziach
21 lip 00:21
henrys: a tak jeszcze √3
21 lip 00:22
yyy:
odp: m(√3−1, √3>
21 lip 00:23
pigor: ..., wyznacz wszystkie wartości parametru m dla
których równanie
√ |x−4|−1= 3−√3m ma dwa rozwiązania dodatnie..
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
no to w swojej "szufladzie" widzę to tak ;
√ |x−4|−1= 3−√3m i 3−
√3m ≥0 ⇔ |x−4|−1 = 9+3m
2−6
√3m i
√3m≤ 3 ⇔
⇔ |x−4|= 3m
2−6
√3m+10 i 3m≤ 3
√3 i w x= 0 |x−4|= 4 ⇒ warunki zadania
spełnia układ nierówności 0< 3m
2−6
√3m+10< 4 i m≤
√3 ⇔
⇔ 3m
2−6
√3m+10 >0 i 3m
2−6
√3m+6< 0 i m≤
√3 ⇔
⇔ m∊R i
√3−1< m<
√3+1 i m≤
√3 ⇔
√3−1< m≤ √3 ⇔
m∊(√3−1;√3>.

21 lip 01:06
 Gdzie jest błąd
Gdzie jest błąd 
 Faktycznie po lewej stronie √x, po prawej coś, nazwijmy to y
√x=y
y≥0 aby był pierwiastek
Jeszcze przy okazji nie wolno tego rysować w przedziale (3,5) gdzie to co jest pod
pierwiastkiem tzn |x−4|−1 jest na minusie ?
Faktycznie po lewej stronie √x, po prawej coś, nazwijmy to y
√x=y
y≥0 aby był pierwiastek
Jeszcze przy okazji nie wolno tego rysować w przedziale (3,5) gdzie to co jest pod
pierwiastkiem tzn |x−4|−1 jest na minusie ?
 Gdy x<4 rysuję √−x+3 tutaj dziedzina to −x+3≥0 ⇔x≤3 czyli od (3,4) też niczego nie będzie
Narysować √x−5 i √−x+3 umiem
Gdy x<4 rysuję √−x+3 tutaj dziedzina to −x+3≥0 ⇔x≤3 czyli od (3,4) też niczego nie będzie
Narysować √x−5 i √−x+3 umiem
 Moja propozycja rozwiązania:
√|x − 4| − 1 = 3 − √3m
Gdy 3 − √3m < 0 mamy równanie sprzeczne
Zakładamy zatem, że m ≤ √3.
Określamy dziedzinę dla x,
|x − 4| − 1 ≥ 0 ⇒ |x − 4| ≥ 1 ⇒ x ∊ (−∞, 3> U <5,∞)
Podnosimy równanie do kwadratu
|x − 4| − 1 = 9 − 6√3m + 3m2
|x − 4| = 3m2 − 6√3m + 10
Rysuję funkcję f(x) = |x − 4|
Na zielono narysowałem skrajne przypadki dla funkcji stałej zależnej od m
Odczytujemy, że 3m2 − 6√3m + 10 musi znajdować się w przedziale <1,4)
No i rozwiązujemy podwójną nierówność
1 ≤ 3m2 − 6√3m + 10 < 4
0 ≤ 3m2 − 6√3m + 9 i 3m2 − 6√3m + 6 < 0
0 ≤ m2 − 2√3m + 3 i m2 − 2√3m + 2 < 0
0 ≤ (m − √3)2 Δ = 4, √Δ = 2, m1 = √3 − 1, m2 = √3 + 1
m ∊ R m∊ (√3 − 1, √3 + 1)
Pamiętam o naszym założeniu na początku otrzymując odpowiedź:
m ∊ (√3 − 1, √3>
=============
Moja propozycja rozwiązania:
√|x − 4| − 1 = 3 − √3m
Gdy 3 − √3m < 0 mamy równanie sprzeczne
Zakładamy zatem, że m ≤ √3.
Określamy dziedzinę dla x,
|x − 4| − 1 ≥ 0 ⇒ |x − 4| ≥ 1 ⇒ x ∊ (−∞, 3> U <5,∞)
Podnosimy równanie do kwadratu
|x − 4| − 1 = 9 − 6√3m + 3m2
|x − 4| = 3m2 − 6√3m + 10
Rysuję funkcję f(x) = |x − 4|
Na zielono narysowałem skrajne przypadki dla funkcji stałej zależnej od m
Odczytujemy, że 3m2 − 6√3m + 10 musi znajdować się w przedziale <1,4)
No i rozwiązujemy podwójną nierówność
1 ≤ 3m2 − 6√3m + 10 < 4
0 ≤ 3m2 − 6√3m + 9 i 3m2 − 6√3m + 6 < 0
0 ≤ m2 − 2√3m + 3 i m2 − 2√3m + 2 < 0
0 ≤ (m − √3)2 Δ = 4, √Δ = 2, m1 = √3 − 1, m2 = √3 + 1
m ∊ R m∊ (√3 − 1, √3 + 1)
Pamiętam o naszym założeniu na początku otrzymując odpowiedź:
m ∊ (√3 − 1, √3>
=============




 graficznie
Rysujesz wykresy :
f(x)= √|x−4|−1 dla x∊ R\ (3, 5)
y=k gdzie k =3−√3*m
Dwa rozwiązania dodatnie są gdy: 0≤k<√3 ⇒
3−√3m≥0 i 3−√3m<√3 ⇒ ......... m∊(√3−1, √3>
graficznie
Rysujesz wykresy :
f(x)= √|x−4|−1 dla x∊ R\ (3, 5)
y=k gdzie k =3−√3*m
Dwa rozwiązania dodatnie są gdy: 0≤k<√3 ⇒
3−√3m≥0 i 3−√3m<√3 ⇒ ......... m∊(√3−1, √3>
