Proszę o wytłumaczenie tego zadanka :)) Krzyś: Rozwiąż układ nierówności: x²≥3x |x²−4x|<4

Mila: x²−3x≥0 −4<x²−4x<4 (1) x*(x−3)≥0⇔x≤0 lub x≥3 ( na osi) x²−4x+4>0 i x²−4x−4<0

	4+4√2
(x−2)2>0 i Δ=16+16=32, x1=		=2+2√2 lub x2=2−2√2⇔
	2

(x∊R\{2} ) i (x∊(2−2√2,2+2√2))⇔ (2) x∊(2−2√2,2+2√2)\{2} Z (1) i (2)⇒x∊(2−2√20>∪<3,2+2√2)

.......: 1/ x²−3x≥0 ⇒x(x−3)≥0 ⇒ x∊(−∞, 0> U <3,∞) 2/ |x²−4x|<4 ⇔ x²−4x<4 i x²−4x> −4 ⇔ x²−4x−4<0 i (x−2)²>0 x²−4x−4<0 , Δ=32 , x=2−2√2 v x= 2+2√2 ⇒ x ∊(2−2√2, 2+2√2) i x∊ℛ\ {2} odp do 2/ : x∊(2−2√2, 2+2√2) \ {2} Jako rozwiązanie układu tych nierówności podaj część wspólną obydwu rozwiązań 1/ i 2/

Mila: Z (1) i (2)⇒x∊(2−2√2,0>∪<3,2+2{2})

Krzyś: Mila dzięki za szczegółowe wyjaśnienie, ale dalej nie pojmuje na jakiej zasadzie wyznaczane są zbiory na osi, mogłabyś mi to wytłumaczyć?

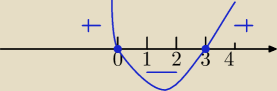
Mila: 1) zbiory na niebiesko to rozwiązanie nierówności : x*(x−3)≥0 to jest nierówność kwadratowa: y=x²−3x wykresem jest parabola skierowana do góry x=0, x=3 − miejsca zerowe wartości nieujemne dla x≤0 lub x≥3 To jasne? Dalej rozumiesz teraz?

Bogdan: Dobry wieczór Mila, dla uczestników tego forum używam adresu mailowgo matura@vp.pl Podaj mi na ten adres swój adres mailowy, chciałbym skontaktować się z Tobą ta drogą.