F
F599: | | 3 | |
Funkcja f określona jest wzorem f(x)= |
| gdzie x∊R |
| | x2+1 | |
Podaj przedział liczbowy, w którym funkcja f jest malejąca
19 lip 14:26
ZKS:
| | x2 + 1 | |
Na początku będziemy rozpatrywać funkcję g(x) = |
| , wtedy xw = 0 oraz współczynnik |
| | 3 | |
przy najwyższej potędze jest dodatni, zatem funkcja maleje dla x ∊ (−
∞ ; 0] natomiast
| | 1 | |
rośnie dla x ∊ [0 ; ∞). Teraz wracając do wyjściowej funkcji widzimy, że f(x) = |
| , |
| | g(x) | |
czyli jest to odwrotność funkcji g(x), więc tutaj funkcja rośnie dla x ∊ (−
∞ ; 0] i
maleje dla x ∊ [0 ;
∞).
19 lip 14:50
Janek191:
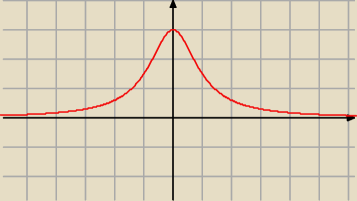
19 lip 14:54
F599: ZKS dziękuję ogromnie
19 lip 14:57
Michcio: Da się to jakoś inaczej zrobić ?
Bo ja np. nie miałem odwrotności funkcji i zależności między monotonicznością funkcji f(x) a
| | 1 | |
|
| a zadanie jest z pierwszego Pazdry |
| | f(x) | |
21 lip 00:20
Godzio:
Teraz w programie jest pochodna, więc może tą drogą?
21 lip 00:23
Michcio: Kurde nie miałem jeszcze tego

21 lip 00:28
Godzio: To zadanie na 2 linijki jeśli to się już umie

A jeśli nie to trzeba się męczyć sposobem
ZKS
21 lip 00:30
Michcio: A pokaż ten sposób na 2 linijki

21 lip 00:31
Godzio:
Funkcja maleje gdy f'(x) < 0 ⇔ −6x < 0 ⇔ x > 0 koniec

21 lip 00:55
ZKS:
Zapomniałem rzeczywiście, że teraz są już pochodne w programie.
| | 6x | |
f'(x) = − |
| , jeżeli f'(x) < 0 to funkcja jest malejąca dla tych argumentów. |
| | (x2 + 1)2 | |
| | 6x | |
− |
| < 0 ⇒ x > 0. |
| | (x2 + 1)2 | |
Funkcja maleje dla x ∊ (0 ;
∞).
21 lip 00:57
john2: Może ktoś wyjaśnić, jak to jest z tymi odwrotnościami?
Bo ja myślałem, że funkcją odwrotną do
jest...
y(x
2 + 1) = 3
x =
√ (3 / y) − 1
a nie...
21 lip 14:37
J:
nie myl pojęcia "funkcji odwrotnej" z "odwrotnością funkcji"
21 lip 14:42
J:
np.: funkcją odwrotną do y = x
3 jest funkcja y =
3√x ,
| | 1 | |
ale jej odwrotnością jest y = |
| |
| | x3 | |
21 lip 14:45
john2: Aha. Dzięki.
21 lip 14:51
Michcio: @J:
Jaki jest wzór na funkcję odwrotną
| | 1 | |
(Odwrotność funkcji to |
| ) a funkcja odwrotna ? |
| | f(x) | |
Da się to wyznaczyć jakoś dla każdej funkcji

21 lip 17:54
Kacper:
Nie każda funkcja posiada funkcję odwrotną do siebie.
21 lip 18:07
Michcio: A jakiś przykład ?
21 lip 19:13
john2: Ja to rozumiem w ten sposób, że po prostu wyznaczasz x ze wzoru funkcji i np.
mając
y = x
3 /
3√
3√y =
3√x3
3√y = x
i zamieniasz teraz literki
3√x = y
Warunek jest taki, żeby funkcja była różnowartościowa (y = x
3 taka jest).
Jeśli funkcja nie jest różnowartościowa, można wyznaczyć (chyba dla każdej funkcji) funkcję
odwrotną, ale tylko w przedziale, w którym jest różnowartościowa.
| | π | | π | |
np. funkcją odwrotną do funkcji y = sinx w przedziale − |
| ≤ x ≤ |
| |
| | 2 | | 2 | |
jest y = arcsinx
Można zauważyć, że dziedziną arcsinx jest zbiór wartości sinx w tym przedziale.
21 lip 20:36
J:
Aby funkcja była odwracalna, musi być funkcją wzajemnie jednoznaczną (bijekcją) ,
czyli musi być jednocześnie różnowartościowa (iniekcja) oraz musi być odwzorowaniem
zbioru X "na" zbiór Y (surjekcja)
22 lip 06:44


 A jeśli nie to trzeba się męczyć sposobem
ZKS
A jeśli nie to trzeba się męczyć sposobem
ZKS


