logarytm z podstawą X Łukasz: Cześć, mam problem z tym logarytmem i nie mam pojęcia jak go rozwiązać. W zadaniu odwrotnym, tj. gdy podstawa logarytmy zamieniona z liczbą logarytmowaną nie mam problemów, ale tu brak pomysłu na rozwiązanie i cały czas wychodzi mi zły wynik. A ma wyjść x należy do przedziału (²₃;1) log_x (⁹₄) < −2

tak sobie mysle :): dziedzina

	9
x−2 <
	4

Łukasz:

	2
No okej. Wychodzi na to, że x >		. Ale skąd 1 na drugim końcu przedziału? Przecież
	3

logarytmu nic z drugiej strony nie ogranicza, oprócz x różnego od 1.

5-latek: To zadanie jest bardzo podchwytliwe gdyż masz tutaj nierownosc i musisz rozpatrzyć dwa przypadki Pierwszy gdy podstawa logarytmu x∊(0,1) ( wiadomo co z e zwrotem nierownosci wtedy Drugi gdy podstawa x∊(1,∞) Ja tak mysle

Mila: x>0 i x≠1 x∊(0,1) funkcja logarytmiczna malejąca

	9
logx(		)<logx(x−2)⇔
	4

9
	>x−2⇔
4

9		1
	>		/*x2
4		x2

9		4
	x2>1 /*
4		9

	4
x2−		>0
	9

	2		2
(x−		)*(x+		)>0 i x∊(0,1) ⇔
	3		3

	2
x∊(		,1)
	3

II przypadek x>1 funkcja rosnąca

	9
logx(		)<logx(x−2)
	4

9
	<x−2
4

Dokończ

tak sobie mysle :): ogranicza to, ze jest malejaca

Łukasz: Ani trochę tego nie ogarniam... Ani tego, ani kolejnego, w którym mam

	9
logx(		)>1
	4

i wychodzi na to, że

	9
x1>
	4

	9
i tyle. Nie ma tutaj żadnej jedynki. A w rozwiązaniu jest x należy do (1;		)
	4

henrys: umiesz zmienić podstawę logarytmu?

1
	<−2
log9/4x

x>1 1<−2log_9/4x log_9/49/4<log_9/4(1/x²) 9/4<1/x² x²<4/9 x<2/3 ale x>1 brak rozwiązań x∊(0,1) 1>−2log_9/4x 1>log_9/4(1/x²) log_9/4(9/4)>log_9/4(1/x²) 9/4>1/x² x²>4/9

	2
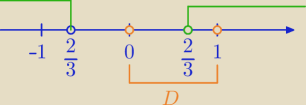
x>2/3 i x∊(0,1)⇒x∊(		,1)
	3

5-latek: Wiec patrz na rozwiaznie Mili z 00:40 dotad az zrozumiesz

henrys: Może tak: Porównaj sobie takie logarytmy log₂8>log₂4 8>4 log_1/28 ? log_1/24 8>4 ale = −3 < =−2