Przekrztałcenia geometryczne Calineczka:): a) Znajdź współrzędne obrazów punktu A=(−2, 3):w symetrii względem punktu (0,0) i w symetrii względem osi x. b) Znajdź współrzędne obrazów punktu B=(2, 4) w symetrii względem punktu (3,1) i w symetrii względem prostej o równaniu y= −1

Rudy: ad a) x'_A = x_A + 2(x_O − x_A) = −2 + 2(0 + 2) = 2 y'_A = y_A + 2(y_O − y_A) = 3 + 2(0 − 3) = −3 A' = (2,−3)

Rudy: względem osi O_x: x''_A = x_A = −2 y''_A = − y_A = −3 A'' = (−2,−3)

Rudy: ad b) w symetrii środkowej względem punktu (3,1) x'_B = x_B + 2(x_O − x_B) = 2 + 2(3 − 2) = 4 y'_B = y_B + 2(y_O − y_B) = 4 + 2(1 − 4) = −2 B' = (4,−2)

Rudy: w symetrii osiowej względem prostej y=−1 x''_B = x_B = 2 y''_B = y_B + 2(y_oś − y_B) = 4 + 2(−1 − 4) = −6 B'' = (2,−6)

Calineczka:): Rudy: ad a) x'A = xA + 2(xO − xA) = −2 + 2(0 + 2) = 2 y'A = yA + 2(yO − yA) = 3 + 2(0 − 3) = −3 A' = (2,−3) A co to jest to xO? skąd to się wzieło?

Rudy: współrzędne środka symetrii, w tym przypadku punktu (3,1)

Rudy: a w pierwszym podpunkcie (0,0)

Calineczka:): Nie rozumiem skąd się to wszystko bierze.... możesz mi to jakoś wyjaśnić? ...

Calineczka:):

Calineczka:):

Rudy: to po kolei, czego nie rozumiesz od początku?

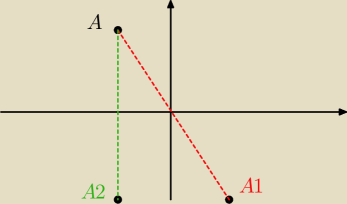
Rudy: najpierw rysunek do punktu pierwszego

Rudy: Najpierw symetria środkowa względem punktu (0,0) Odległość punktu A od punktu O musi być taka sama jak punktu O od punktu A' (na obrazku A1) Najłatwiej zdefiniować sobie wektor AO i potem taki sam wektor przyłożyć do punktu O żeby znaleźć obraz A' w tej symetrii. Punkt A ma współrzędne (−2, 3), wektor AO = [2, −3] Przykładając ten wektor do punktu O otrzymujemy (0,0) + [2,−3] = (2, −3) = A'

Rudy: użyłem wektora bo te punktu leżą na jednej prostej, należy zachować kierunek

Rudy: Symetria względem prostej O_x zamienia rzędną (y_A) na przeciwną, przy czym odcięta (x_A) zostaje taka sama. Wtedy punkt A (−2,3,) w symetrii względem osi O_x ma obraz A' (−2,−3)

Calineczka:): oki teraz rozumiem jak zobaczyłam obrazek to wiem o co chodzi

Calineczka:): A to drugie jak będzie rozrysowane? bardziej przydaje mi sie obrazek wzgledem punku wiem ale tego y= −1 niebardzo

zet: Pomogę

zet: Ok już masz wyjaśnione

Calineczka:): więc jak?

Rudy: rysuję

Calineczka:): Oki dziękuje bardzo za pomoc

Calineczka:): Hmm przepraszam że tak mące ale ja wole mieć zadania tak rozpisane jakby to napisać jak "głąbkowi" bo wtedy wiem skad co sie wzielo i rozumiem tak mnie uczyli i chce dalej sie tak uczyc moze dziwne podejscie ale nie lubie skrótami

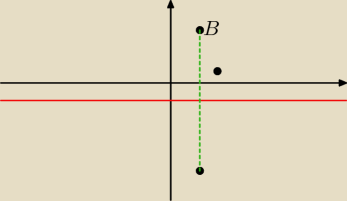
Rudy: Odległość punktu B od prostej y = −1 jest y_B − (−1) = 4 + 1 = 5 i o tyle w dół należy szukać obrazu B' w symetrii osiowej Odcięta (x_B) się nie zmienia. Stąd: x''_B = x_B = 2 y''_B = y_B + 2(y_oś − y_B) = 4 + 2(−1 − 4) = −6 B'' = (2,−6)

Rudy: Do wartości y_B dodajemy dwa razy wektor [0, −5], bo 5 jest odległością B od osi y = −1, a ponieważ jest pozioma to poruszamy się wzdłuż osi O_y Nie wiem czy już nie za dużo "natłumaczyłem",żeby się nie stało zbyt skomplikowane. Oczywiście inaczej, bardziej skomplikowanie, należałoby podejść gdyby była to symetria względem jakiejś dowolnej prostej y = ax + b. Należy wtedy znaleźć odległość punktu od prostej, znaleźć rzut punktu na prostą, wyznaczyć wektor i dodać go dwa razy. Mechanizm ten sam, tylko obliczenia bardziej zawiłe. Zrozumiałaś Calineczko?

Calineczka:): Ojoj myślałam myślalam czytałam czytałam i w końcu zrozumialam Dziękuje bardzo za cierpliwość

Rudy: powodzenia