promień kulu i stosunek bartek: http://img239.imageshack.us/img239/2519/tapr420.gif Jeżeli promień piłki wynosi r to ile wynosi ^a_b

xx:

	2
a/b=		*(1 + √22)
	7

bartek: skąd ten wynik?

henrys:

√2
2

bartek: A skąd te wyniki?

henrys: Obliczyłem, chcesz rozwiązanie?

bartek: Możesz pokazać bo xx ma inny

henrys: a wiesz, który jest poprawny?

bartek: niestety nie mam odp

henrys: Ok tylko trochę to zajmie bo nie narysuje tego

bartek: spoko może xx tez napisze czemu ma taki wynik

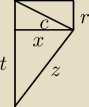
henrys: Promień dużego okręgu =b, promień małego okręgu =r Niech c=1/2a=1/2b−r b=2c+2r a=2c

a		2c		c
	=		=
b		2c+2r		c+r

Ponieważ okręgi małe są odpowiednio styczne do okręgów dużych więc z=c+2r t=a−r=2c−r Dostajemy układ równań x²=c²−r² x²+(2c−r)²=(c+2r)² c²−r²+4c²−4cr+r²−c²−4cr−4r²=0 −4r²−8cr+4c²=0 r²+2cr−c²=0 rozwiązujemy wzgledem r Δ=8c² √Δ=2c√2

	−2c−2c√2
r1=		<0, nie spełnia założeń bo c>0, r>0
	2

r=c√2−c

a		c		1		√2
	=		=		=
b		c+c√2−c		√2		2

henrys: oj tam na początku, oczywiście promień dużego okręgu to 1/2b

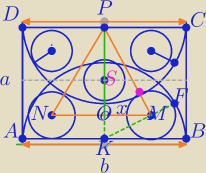
Mila: Rysunek dla Henrysia. Piłeczki trochę nie wyszły, ale można coś zobaczyć. Dopisz dla Bartka w których trójkątach stosujesz tw. Pitagorasa.

henrys: Dzięki Mila, nawet na kartce tego nie narysowałem ΔKMO i ΔOPM

Mila: Myślę, że już dla Bartka będzie wszystko jasne.