granica arctgx/x john2:

	arctgx
limx−>0
	x

	arctgx
Wiem, że jest wzór gotowy limx−>0		= 1,
	x

ale mam tę granicę obliczyć, nie znając tego wzoru. Jest tylko wskazówka: "położyć arctgx = α" No więc kładę:

	α		α
limx−>0		= limx−>0		= i co teraz?
	x		tgα

ZKS: Teraz, jeżeli x → 0 to α → ...

john2: jeżeli x − > 0 to tgα −> 0 a wtedy α −> 0 ?

ZKS: Tak. Dalej już chyba wiadomo jak?

john2: Tak jest. Dziękuję.

Mariusz:

	sin(α)
tan(α)=
	cos(α)

sin(α)
	Wobec parzystości można brać tylko wartości dodatnie α
α

Granice liczysz z trzech ciągów

john2:

	sinα
Nie wiem, czy nadążam, ale przy limα−>0		już tym razem, przyznam się bez bicia,
	α

pozwoliłem sobie skorzystać ze wzoru. Nie wiem, jak to ruszyć trzeba ciągami/funkcjami.

Mariusz:

	sin(α)
Aby wykazać że limα→0		=1
	α

korzystasz z twierdzenia o trzech ciągach

J:

	cosx
Jako student, masz pełne prawo napisać ... = lim		= 1
	1

john2: Nie jestem studentem Prawdę mówiąc, nie lubię reguły de l'Hospitala. Za bardzo ułatwia sprawę (choć to raczej dobrze). Ja lubię dociekać.

john2: Mariusz, mam to zamienić na coś takiego?

	1   sin   n
limn−>∞
	1   n

Mila: Co chcesz zamienić na taka postać?

john2:

	sinα
limα−>0
	α

żeby skorzystać z tw. o trzech ciągach, bo to chyba nie jest ciągiem

Mila: To jest tzw. granica specjalna . Jeżeli nie masz w pleceniu wykaż, to korzystaj z gotowej. http://smurf.mimuw.edu.pl/node/108

Mariusz: Tutaj z Hospitala nie można skorzystać bo jak policzysz pochodną sinusa ? Do policzenia pochodnej sinusa potrzebna jest właśnie ta granica W otoczeniu zera prawdziwe są nierówności sin(x)<x<tan(x) Powinieneś je przekształcić aby otrzymać to co trzeba

john2: sinx < x

sinx
	< 1
x

mam ograniczenie z góry, a co z dołem?

Mariusz: sin(x)<x<tan(x) | : sin(x)

	x		1
1<		<		(biorąc odwrotności)
	sin(x)		cos(x)

	sin(x)
cos(x)<		<1
	x

Skrajne ciągi/funkcje dążą do jedności więc wobec prawdziwości nierówności środkowa też musi

john2: Ok. Dzięki.

Mila: lim_x→0arctgx=0 arctgx=α x=tgα

	α		α
limα→0		=limα→0		=
	tgα		sinα   cosα

	α
=limα→0		*cosα=1*1=1
	sinα

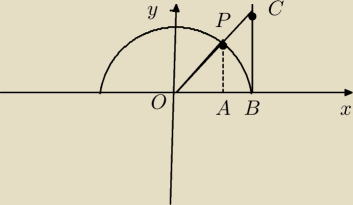
Mariusz: PB = x AP=sin(x) OA=cos(x) BC=tan(x) OB=OP=1 , Dla uproszczenia przyjmijny że to jest półokrąg o promieniu jednostkowym

Mariusz: Mila dobrze by było aby chociaż raz policzył tą granicę aby wiedział dlaczego ona akurat tyle wynosi

Mariusz: Policzmy może pochodną sinusa

	sin(x+Δx)−sin(x)		sin(x)cos(Δx)+cos(x)sin(Δx)−sin(x)
limΔx→0		=limΔx→0
	Δx		Δx

	sin(x)(cos(Δx)−1)+cos(x)sin(Δx)
=limΔx→0
	Δx

	sin(x)(cos(Δx)−1)		cos(x)sin(Δx)
=limΔx→0		+limΔx→0
	Δx		Δx

	cos(Δx)−1		sin(Δx)
=sin(x)limΔx→0		+cos(x)limΔx→0
	Δx		Δx

	Δx		Δx		Δx
=sin(x)limΔx→0U{cos2(		)−sin2(		)−cos2(		)−sin
	2		2		2

	Δx
2(		)}{Δx}+
	2

	sin(Δx)
cos(x)limΔx→0
	Δx

	Δx   −2sin2( )   2		sin(Δx)
=sin(x)limΔx→0		+cos(x)limΔx→0
	Δx		Δx

	−Δx		Δx   sin( )   2
=sin(x)limΔx→0		limΔx→0(		)2+
	2		Δx   2

	sin(Δx)
cos(x)limΔx→0
	Δx

No i jakiej granicy potrzebujemy do policzenia pochodnej sinusa ?

john2: No raczej nie skorzystamy teraz z de l'Hospitala, bo będziemy biegać w kółko. Chyba rozumiem.

Mariusz: john2 cieszę się że rozumujesz Właśnie to usiłowałem im napisać ale oni nie chcieli tego czytać Co do uczenia się wielu wzorków na pamięć , no nie róbmy z matematyki przedmiotu humanistycznego . Uważam że przynajmniej raz powinieneś tą granicę policzyć Później gdy będziesz wiedział dlaczego ta granica akurat tyle wynosi to możesz ją dla skrótu wykorzystywać jako gotową

Fru: Mariusz nie fiksuj. Przerost formy nad treścią?

Mariusz: Pochodnych też nie liczycie używając granic a później nadużywacie Hospitala Jak się uczy zbyt wielu rzeczy na pamięć to łatwiej zapomnieć i wtedy nie będzie wiedział jak takie rzeczy liczyć

Mila: Najpierw w szkole tłumaczy się co to jest pochodna, potem liczy się pochodne z definicji, następnie podaje się wzory (najczęściej obliczone z definicji). W zadaniach korzysta się z wzorów, o ile nie ma polecenia " Oblicz z definicji...

Mariusz: Tak ale chyba jasiek tej granicy nie liczył bo nie wiedział dlaczego ona dąży do jedynki

Mariusz: jest równa jedynce funkcja dąży do jedynki