geometria bimbam: Hej. Kolejne zadanie, z którym mam problem Przez punkt przecięcia prostych: x−1=0 oraz x+y−2=0 poprowadź prostą ograniczającą wraz z osiami układu współrzędnych trójkąt o polu 1. Obliczyłem, że ten punkt to oczywiście P(1,1) Trzeba zastosować tu równanie odcinkowe prostej

x		y
	+		= 1
a		b

S=1

	1
1=		IabI //
	2

2=IabI ab= 2 v ab=−2 no i tu nie wiem co dalej. Odpowiedź ma coś wspólnego ze wzorem x+y−2=0, bo ma ona postać (1−√3)x+(1+√3)y−2=0 lub (1+√3)x+(1−√3)y−2=0 Jak obliczyć x oraz y

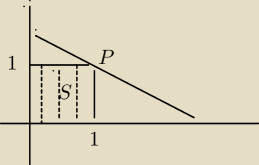AS: Według moich rozważań pole wskazanego trójkąta nie może równać się 1 tylko więcej. S = 1 j² , a pole trójkąta będzie zawsze większe od S.

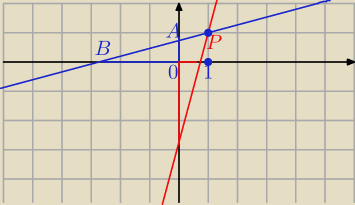Janek191: P = ( 1, 1) y = a x + b przechodzi przez P , więc 1 = a*1 + b ⇒ b = 1 − a zatem y = a x + 1 − a −−−−−−−−−−−−− Dla x = 0 mamy y = 1 − a A = ( 0, 1 − a) =========== Dla y = 0 mamy 0 = a x + 1 − a a x = a − 1

	a − 1
x =
	a

	a −1
B = (		, 0 )
	a

================= Pole

	a −1
P = 0,5*I		I*( 1 − a) = 1
	a

	a − 1
I		I *(1 − a) = 2
	a

	a −1		2
I		I =
	a		1 −a

a −1		2		a −1		2
	= −		lub		=
a		1 −a		a		1 −a

− 2a = a −a² − 1 + a lub 2a = a −a² − 1 + a a² − 4 a + 1 = 0 lub 0 = − a² − 1 − sprzeczność Δ = 12 =4*3 √Δ = 2√3

	4 − 2√3
a =		= 2 − √3 więc b = 1 − a = − 1 + √3
	2

lub

	4 + 2√3
a =		= 2 + √3 więc b = 1 − a = − 1 − √3
	2

Równania szukanych prostych: y = ( 2 − √3) x − 1 + √3 y = ( 2 + √3) x − 1 − √3 ====================

henrys: ciekawe zadanie

bimbam: dziękuję za pomoc