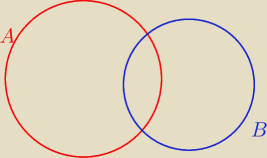
Naiwna teoria mnogości Przemysław: Czy jeśli (A⊂A∪B)⋀(A≠A∪B) to A\B≠∅? TAK/NIE TAK − wtedy A\B≠∅ NIE − wtedy A\B=∅ Poprawna odpowiedź to NIE. Nie rozumiem dlaczego Przecież jeżeli miałbym coś takiego jak na rysunku to prawdą są założenia, a jednak A\B≠∅ Gdzieś pewnie jakąś głupotę robię, ale tego nie widzę, proszę o pomoc.

PW: A co by było, gdyby A = ∅ ?

PW: ... albo A byłby niepusty, ale zawarty w B i różny od B ?

Przemysław: Nie bardzo rozumiem... No bo przeciez nie mamy napisane, ze zachodzi któryś z tych warunków... Na tej samej zasadzie mogę zapytać "a co jak jest tak jak na rysunku?". Co by znaczyło ze obie opcje są możliwe przy tylko tych założeniach z zadania, wiec cos pewnie przegapiam.

PW: W założeniach nie ma nic o zbiorze A poza tym co napisane. Masz odpowiedzieć na pytanie "czy podana implikacja jest zdaniem prawdziwym". Prawdziwym we wszystkich możliwych wypadkach. A tak nie jest.

Przemysław: Ok! dziękuję bardzo