geometria bimbam: Hej Mam zadanie: znaleźć punkt jednakowo odległy od prostej x+y+1=0 i od punktów A(1,1) B(2,1). Zrobiłem rysunek, ale nie wiem co dalej z tym robić. W podpowiedziach jest napisane, że współrzędne szukanego punktu P(x,y) spełniają układ równań:

	(x+y+1)2
(x−1)2+(y−1)2=(x−2)2+(y−1)2=
	2

// nad x,y w powyższych wzorach są "daszki", ale to chyba nie są wektory// Ta podpowiedź nic mi jednak nie pomaga. Może ktoś zna jakieś inne rozwiązanie Odpowiedź to:

	3		9
P1(		,		+ √6 )
	2		2

	3		9
P2(		,		− √6 )
	2		2

ZKS: Mi wychodzą inne odpowiedzi.

ZKS: Oznaczmy sobie ten szukany punkt jako C (x ; y), wtedy z treści zadania wynika, że |AC| = |BC|, następnie liczymy odległość d tego punktu od prostej x + y + 1 = 0 i to ma być równe tyle co |AC| = d, albo |BC| = d.

PW: Punkty jednakowo oddalone od A i od B leżą na symetralnej tego odcinka. Gdyby cyrklem szukał takich punktów, to kreśliłby okrąg o środku A i promieniu r oraz okrąg o środku B i tym samym promieniu r. Tam, gdzie przecięły się te okręgi, mamy dwa punkty jednakowo oddalone od A i od B (jeżeli w ogóle się przecięły, czyli jeżeli r jest dostatecznie duży − wykonaj samodzielnie konstrukcję dla kilku r). To rozumowanie uzasadnia konieczność spełniania równania (1) (x̂−1)² + (ŷ−1)² = r² = (x̂−2)² + (ŷ−1)² przez współrzędne x̂, ŷ punktów leżących w jednakowej odległości od A i od B (są to równania okręgów o tym samym promieniu r i środkach A = (1, 1) oraz B = (2,1). Te daszki nad x i y są po to, żeby odróżnić współrzędne punktów symetralnej od współrzędnych dowolnych punktów płaszczyzny. Pomyśl teraz, skąd wzięło się jeszcze przyrównanie tych liczb z (1) do

	|x̂+ŷ+1|
(2) (		)2
	√2

henrys: p₁(3/2,9/2−2√6) p₂(3/2,9/2+2√6)

bimbam: dzięki za wypowiedzi. Już zabieram się za czytanie.

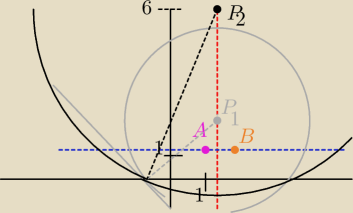
bimbam: PW, Twój opis trochę pomógł. Wiem skąd się wzięła lewa strona równania, ale prawa − niestety nie. 4,5+√6 ≈ 6,9 4,5−√6 ≈ 2,05

	3		3
Czyli w punktach P1(		, 6,9 ) P2(		, 2,05 ) będą te środki okręgów.
	2		2

Chyba zły rysunek wykonałem

bimbam: zauważyłem, że u mnie promienie są różne

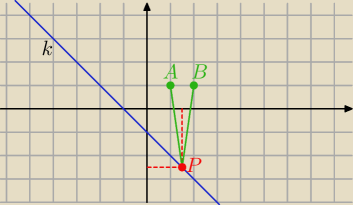
monia: k: y= −x−1 to P(x, −x−1) |AP|²=|BP|² ...............

	3		5
Odp: P(		, −		)
	2		2

Sprawdź czy na pewno dobrze podajesz współrzędne punktów A i B

bimbam: dzięki monia współrzędne podałem prawidłowo, tj. A(1,1) B(2,1)

PW: Pierwsze dwa człony równości to − jak już rozumiesz − równość kwadratów odległości szukanego punktu od A i od B. Trzeci człon równości to kwadrat odległości punktu (x̂, ŷ) od prostej x + y + 1 = 0 (specjalnie napisałem w takiej postaci, żeby ten wzór na odległość był widoczny, a nie tak jak w podpowiedzi w książce).

Bogdan: Wtrącę swoje 3 grosze A(1, 1), B(2, 1), prosta k: x + y + 1 = 0,

	|x0 + y0 + 1|
r = |SA|, r = |SB|, r =		− odległość punktu S od prostej k
	√1 + 1

S(x₀, y₀) − szukany punkt

	3
r2 = |SA|2 = |SB|2 ⇒ (x0−1)2 + (y0−1)2 = (x0−2)2 + (y0−1)2 ⇒ x0 =
	2

	3		5
r2 = |SA|2 = (		− 1)2 + (y0 − 1)2 ⇒ r2 = y02 − 2y0 +
	2		4

oraz

	5   | + y0|2   2		25   y02 + 5y0 +   4
r2 =		=
	2		2

	5		25   y02 + 5y0 +   4		15
y02 − 2y0 +		=		⇒ y02 − 9y0 −		= 0
	4		2		4

Δ = 96, √Δ = 4√6, y₀ = ... lub y₀ = ...

ZKS: monia a kto powiedział, że ten punkt należy do prostej?

Bogdan:

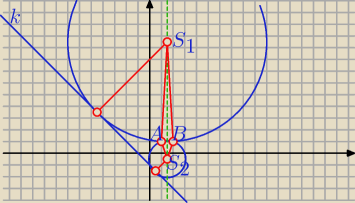
	3
Szukany punkt leży na prostej x =		i jest środkiem okręgu przechodzącego
	2

przez punkty A i B oraz stycznego do prostej k: x + y + 1 = 0. Są dwa takie okręgi spełniające warunki zadania, zadanie ma więc dwa rozwiązania.S₁ i S₂

bimbam: PW, Tak się właśnie zastanawiałem dlaczego wpisałeś w mianowniku równości po prawej stronie √2 skoro w podpowiedziach jest tylko 2.Te kilka zdań, które właśnie dodałeś, rozjaśniło sytuację. Bogdan, Twoje kompletne rozwiązanie jest bardzo pomocne. Rysunku bym sam nie zrobił. Dziękuję wszystkim za pomoc

monia: Sorry (źle przeczytałam treść zadania) Przeczytałam : znajdź punkt na prostej równo odległy od punktów A i B Stąd taki rysunek i rozwiązanie

Maniek: monia dotknięta jest powszechną bolączką wielu współczesnych osobników, to nieumiejętność czytania ze zrozumieniem tego, co czytają. Jak można coś źle przeczytać? Litery i znaki pisane układają się przecież w słowa, problemem jest rozumienie przeczytanego tekstu.