Zbiór wartości
Patryk97: Oblicz zbiór wartości f(x)=|sinx|+|cosx|
10 lip 14:54
PW: Wskazówka. Wyznacz zbiór wartości funkcji
g(x) = f2(x)
10 lip 19:22
Mila:
10 lip 21:26
patryk97: Czyli:
g(x)=(|sinx|+|cosx|)2=sin2x+2|sinx|*|cosx|+cos2x?
10 lip 21:30
Saizou :
tak
a dalej sin2x+cos2x+|2sinxcosx|=1+|sin2x|, zatem....
10 lip 21:38
x&y:
0≤|sinx|≤1
0≤|cosx|≤1
+−−−−−−−−−−−−−−
0≤|sinx|+|cosx|≤2
ZW= <0,2>
10 lip 21:40
Saizou :
x&y to co piszesz jest fałszem,
podaj mi wartość x taką, że f(x)=0
ODp. to ZW=[1,√2]
10 lip 21:43
Joe Black: hmmm...
−1≤sinx≤1
−1≤sin2x≤1
0≤|sin2x|≤1
1≤|sin2x|+1≤2
Zwf: y∊<1,2>
10 lip 21:44
Saizou :
Kamilu to dziedzina funkcji g(x)=f2(x) , zatem....
10 lip 21:45
Joe Black: Masz rację
10 lip 21:46
x&y:
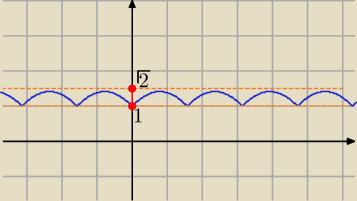
ZW=
<1,√2> 
10 lip 21:51
pigor: ..., dlatego zapomniałeś o "spier...
wiastkowaniu"
10 lip 21:52
Joe Black: 
, dobrze że jest
Saizou na straży
10 lip 21:58
Saizou :
Nudzi mi się w wakacje, więc do czasu do czasu tutaj zaglądam
10 lip 22:02
patryk97: Odpowiedź dobra, ale czy można tak sobie bez obaw pierwiastkować zbiór funkcji?
11 lip 10:45
patryk97: Zbiór wartości funkcji*
11 lip 10:55
PW: Można. Zbiór wartości funkcji f na pewno jest zawarty w R+ (wystarczy spojrzeć na definicję
f(x)).
11 lip 11:04
ZKS:
Przecież |sin(x)| + |cos(x)| = ||sin(x)| + |cos(x)|| i stąd mamy
√[|sin(x)| + |cos(x)|]2 = √sin2(x) + 2|sin(x)cos(x)| + cos2(x) = √|sin(2x)| + 1.
11 lip 11:22