objętość kuli opiasanej na stozku Konrad: Oblicz objętość kuli opisanej na stożku, którego przekrój osiowy jest trójkątem równobocznym o boku mającym długość 2cm. Może mi ktos napisac jak to rozwiązać albo chociaż skąd wyliczyć R?

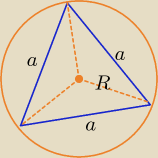
Bogdan: Jaki jest wzór na długość promienia okręgu opisanego na trójkącie równobocznym o boku a?

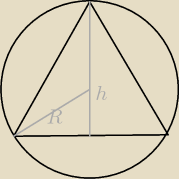
Rudy: W przekroju mamy trójkąt równoboczny i opisany na nim okrąg.

	2
Promień okręgu opisanego na trójkącie równobocznym to		jego wysokości czyli:
	3

	2		a√3		a√3		2√3
R =		*		=		=
	3		2		3		3

Objętość kuli:

	4		4		2√3		32√3π
V =		*π*R3 =		*π*{		}3 =
	3		3		3		27

Bogdan: Warto zapamiętać wzory i nie korzystać z pośrednictwa wysokości w trójkącie rownobocznym: R − długość promienia okręgu opisanego na trójkącie równobocznym, r − długość promienia okręgu wpisanego w trójkąt równoboczny,

	1
R =		a√3, R = 2r,
	3

	1		1
r =		a√3, r =		R
	6		2