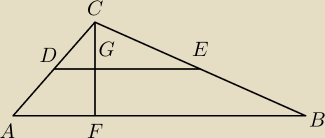
 Dane: |AB|=12, |DE|=8 , |CF| = 6
Szukane: PABED
Rozwiązanie:
ΔDCE ∼ ΔACB (cecha kkk)
Dane: |AB|=12, |DE|=8 , |CF| = 6
Szukane: PABED
Rozwiązanie:
ΔDCE ∼ ΔACB (cecha kkk)
| |DE| | |CG| | ||
= | |||
| |AB| | |CF| |
| 8 | |CG| | ||
= | |||
| 12 | 6 |
| |AB| + |DE| | ||
PABED = | * |GF| | |
| 2 |
| 12 + 8 | ||
PABED = | * 2 = 20 | |
| 2 |
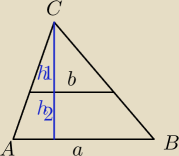 Mam jeszcze jedno podobne zadanie:
Poprowadzono prostą k równoległą do boku AB trójkąta ABC.
W jakim stosunku podzieliła ona wysokość trójkąta,
jeżeli trójkąt podzieliła na dwie figury o równych polach?
Rozwiązuję przez układ równań:
Z podobieństwa trójkątów: h1h2 = ba
Z równości pól h1*b=(a+b)h2
I mam problem z wymyśleniem innych równań do tego..
Mam jeszcze jedno podobne zadanie:
Poprowadzono prostą k równoległą do boku AB trójkąta ABC.
W jakim stosunku podzieliła ona wysokość trójkąta,
jeżeli trójkąt podzieliła na dwie figury o równych polach?
Rozwiązuję przez układ równań:
Z podobieństwa trójkątów: h1h2 = ba
Z równości pól h1*b=(a+b)h2
I mam problem z wymyśleniem innych równań do tego..
| (h1+h2)a | 2P | a | h2 | a | b | ||||||
= | ⇒ | + | = 2 / * | ⇔ | |||||||
| h1b | P | b | h1 | b | a |
| h2 | b | |||
⇔ 1 + | = 2 | ⇒ np. h2 : h1 = 2 ba − 1 = 1a (2b−a) . ...  | ||
| h1 | a |

| bx | 1 | a(x+y) | |||
= | * | ||||
| 2 | 2 | 2 |
| x | a | ||
= | |||
| y | 2b−a |
| bx | a+b | ||
= | *y | ||
| 2 | 2 |
| x | a+b | ||
= | |||
| y | b |
| a | a+b | ||
= | |||
| 2b−a | b |
| x | b√2+b | ||
= | =√2+1 | ||
| y | b |
| h1 | |
=√2+1 | |
| h2 |
| (h1+h2)a | 2P | a2 | h2 | a | a | ||||||
= | = | ⇔ (1+ | ) | = 2= ( | )2 ⇒ | ||||||
| h1b | P | b2 | h1 | b | b |
| a | ||
⇒ | = √2 i (1+x)√2= 2 /*√2 ⇒ 2(1+x)= 2√2 ⇒x= √2−1 | |
| b |
| 1 | 1 | |||
..., oczywiście stąd | =h1 : h2 = | =√2+1. ...  | ||
| x | √2−1 |
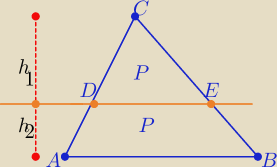 No to ja ... jeszcze krócej ( bez x−ów , bez a i b
Trójkąty ABC i DEC są podobne w skali s>0
No to ja ... jeszcze krócej ( bez x−ów , bez a i b
Trójkąty ABC i DEC są podobne w skali s>0
| 2P | h1+h2 | h2 | h2 | |||||
to s2= | =2 ⇒ s=√2 to : | =s ⇒ 1+ | =√2 ⇒ | =√2−1 | ||||
| P | h1 | h1 | h1 |
| h1 | ||
⇒ | =√2+1 | |
| h2 |





