wektory bimbam: hej Uczę się wektorów. Póki co rozumiem tylko najprostsze przykłady. Mam takie zadanie, którego nie potrafię do końca rozwiązać. Dane są dwa wektory a^→=[1,2−2] oraz b^→=[2,3,6]. Znaleźć współrzędne wektora c^→

	21
o długości		dzielącego kąt między wektorami a→ oraz b→.
	5

W podpowiedziach jest napisane, że szukany wektor c^→ ma kierunek

	1		1
wektora e→ =		a→ +		b→
	a		b

Zatem liczę sobie długość a oraz b. IaI=√ 1 + 4 + 4 =3 IbI=√ 4 + 9+ 36 =7

	1		1
potem liczę e→, więc mam e→=		[1,2−2] +		[2,3,6].
	3		7

	1		2		−2		2		3		6
e→= [		,		,		] + [		,		,		]
	3		3		3		7		7		7

	13		23		4
e→= [		,		,		,]
	21		21		21

Następnie autor podpowiada, by skorzystać z warunku równoległości wektorów, czyli

ux		uy		uz
	=		=
vx		vy		vz

No i nie wiem jak dalej liczyć Czy ktoś mógłby sprawdzić, czy to co do tej pory napisałem, jest prawidłowe

	4
Odpowiedź ze zbioru to c→=[4,		, 1 ]
	5

bimbam: aha: polecenie mówi, że c^→ dzieli kąt między wektorami a oraz b na połowy

bimbam:

Mila: Na razie dobrze zrobiłeś, a wiesz dlaczego tak trzeba zrobić?

	21
Znormalizuj wektor e i pomnóż przez		, ale nie wyjdzie podana odpowiedź.
	5

Pewnie jakiś minus zgubiony w podanych wektorach.

bimbam: dziękuje Mila za pomoc póki co rozumiem mniej więcej skąd się bierze co. W linku zawierającym rozwiązanie podobnego zadania autorka rozwiązania mówi, że "Jeśli szukam rzutu prostokątnego wektora a^→ na prostą o kierunku wektora b^→, to jest to to samo co rzut prostokątny wektora a^→ na wektor b^→"

	1		1
Zatem podany w podpowiedział wzór e→ =		a→+		b→
	a		b

wynika ze wzoru u^→ = rzut wektora na wektor

	a→ * b→
u→ =		* b→ // w liczniku jest iloczyn skalarny
	Iu→ I2

w poniższym linku osoba osoba przedstawia podobne zadanie i jest w nim podany ww. wzór na .u^→ https://www.youtube.com/watch?v=1BxgNCvEpQw&index=4&list=PLWWDiQscgVtexxG_pRx-4e2Bfeg_NNuZ_ Wydaje mi się, że dobrze przepisałem współrzędne wektora. Zapomniałem tylko przecinka Dane są dwa wektory a^→=[1,2,−2] oraz b^→=[2,3,6]. znormalizować wektor to znaczy podzielić jego współrzędne przez normę II e II

	714
Jeśli tak, to wychodzi mi coś takiego II e II =
	21

wektor e^→ po znormalizowaniu ma współrzędne

	13		23		4
e→=(		,		,		)
	714		714		714

c^→ nie wyjdzie taki jak w odpowiedziach

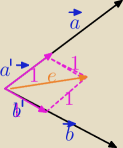Mila: Chodzi o to, że znormalizowano najpierw wektory a i b, zatem obydwa wektory a' i b' mają długość równą 1, "zaczepione" w jednym punkcie są bokami rombu. Przekątne rombu są dwusiecznymi kątów. Wektor będący sumą dwóch wektorów o takich samych długościach tworzy jednakowe kąty z tymi wektorami i leży w tej samej płaszczyźnie wyznaczonej przez wektory a i b.

bimbam: Dziękuję