B.
B4N4NI | BF4: W Δprostokątnym przeciwprostokątna ma długość 30. Oblicz odległość środka ciężkości tego Δ od
wierzchołka kąta prostego.
Dlaczego wychodzi 10, mi wychodzi 15
8 lip 18:15
Mila:
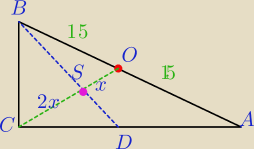
Środkowe Δ dzielą się w stosunku 2:1 licząc od wierzchołka.
S− środek ciężkości Δ.
|OC|=15
3x=15
x=5
|CS|=2x=10
8 lip 18:24
B4N4NI | BF4: A czemu |OC|=15 ?
Jak to udowodnic
8 lip 18:29
Benny: Poczytaj o okręgu opisanym na trójkącie prostokątnym.
8 lip 18:36
Mila:
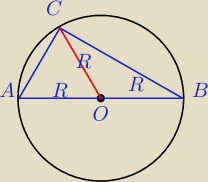
Środek okręgu opisanego na Δprostokątnym leży w środku przeciwprostokątnej.
OC− środkowa Δ poprowadzona z wierzchołka kąta prostego jest równa promieniowi okręgu
okręgu opisanego na tym Δ.
8 lip 19:33
B4N4NI | BF4: Nie.
Mam zadanie żeby udowodnić że jeżeli środkowa Δ równa się połowie boku do którego została
poprowadzona to trójkąt jest prostokątny

Okręgów jeszcze nie miałem

8 lip 21:04
Mila:
Czego dotyczy "nie".
W której jesteś klasie?
8 lip 21:08
B4N4NI | BF4: Dobra już wiem...
Kątami można to udowodnić

1., i robię pierwszego pazdrę przed okręgami
Mozna to udowdnić poprzez kąty w trójkącie (bo tam będą dwa trójkąty prostokątne)
8 lip 21:19
B4N4NI | BF4: a ty w której klasie
8 lip 21:20
Eta: W 6 podstawówki

8 lip 21:23
B4N4NI | BF4: dzieci

dobra ide grac elo
ale to pierwsze zadanie faktycznie skopalem a było bardzo proste
8 lip 21:24
Mila:
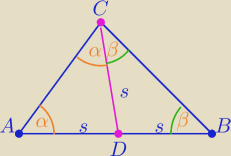
CD=s− środkowa
ΔACD, ΔBCD− Δrównoramienne
W ΔABC:
α+α+β+β=180
o⇔
α+β=90
o⇔
ΔABC− Δprostokątny o kącie prostym w wierzchołku C
===========================================
8 lip 21:25
Mila:
Jeżeli zadaję pytanie o klasę, to po to, aby wiedzieć w jaki sposób Ci wytłumaczyć.
Bez żadnych podtekstów. O okręgach opisanych na trójkącie jest w programie klasy I GM.
8 lip 21:29
 Środkowe Δ dzielą się w stosunku 2:1 licząc od wierzchołka.
S− środek ciężkości Δ.
|OC|=15
3x=15
x=5
|CS|=2x=10
Środkowe Δ dzielą się w stosunku 2:1 licząc od wierzchołka.
S− środek ciężkości Δ.
|OC|=15
3x=15
x=5
|CS|=2x=10
 Środek okręgu opisanego na Δprostokątnym leży w środku przeciwprostokątnej.
OC− środkowa Δ poprowadzona z wierzchołka kąta prostego jest równa promieniowi okręgu
okręgu opisanego na tym Δ.
Środek okręgu opisanego na Δprostokątnym leży w środku przeciwprostokątnej.
OC− środkowa Δ poprowadzona z wierzchołka kąta prostego jest równa promieniowi okręgu
okręgu opisanego na tym Δ.
 Okręgów jeszcze nie miałem
Okręgów jeszcze nie miałem 
 1., i robię pierwszego pazdrę przed okręgami
Mozna to udowdnić poprzez kąty w trójkącie (bo tam będą dwa trójkąty prostokątne)
1., i robię pierwszego pazdrę przed okręgami
Mozna to udowdnić poprzez kąty w trójkącie (bo tam będą dwa trójkąty prostokątne)

 dobra ide grac elo
ale to pierwsze zadanie faktycznie skopalem a było bardzo proste
dobra ide grac elo
ale to pierwsze zadanie faktycznie skopalem a było bardzo proste
 CD=s− środkowa
ΔACD, ΔBCD− Δrównoramienne
W ΔABC:
α+α+β+β=180o⇔
α+β=90o⇔
ΔABC− Δprostokątny o kącie prostym w wierzchołku C
===========================================
CD=s− środkowa
ΔACD, ΔBCD− Δrównoramienne
W ΔABC:
α+α+β+β=180o⇔
α+β=90o⇔
ΔABC− Δprostokątny o kącie prostym w wierzchołku C
===========================================