Pole trójkąta
ugabuga: Obliczyć pole powierzchni trójkąta o wierzchołkach: A(2, 1, −1) B(−1, −2, 2) C(3, 0, 1)
może być tylko wynik
7 lip 22:09
5-latek:
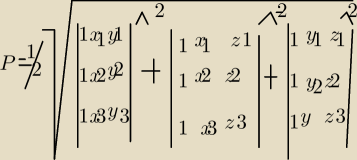
Ma by x
1 x
2 i x
3 tez y
1,y
2y
3 i to samo wspolrzedne z
1 z
2 z
3
wyznaczniki pod pierwiastkiem do potęgi drugiej
7 lip 22:54
Saizou :
| | 3 | |
jak się nie walnąłem to P= |
| √14 |
| | 2 | |
7 lip 22:55
Eta:
Ten trójkąt jest prostokątny
|AC|=
√6 , |BC|=
√21 , |AB|=
√27
7 lip 22:56
Eta:

7 lip 22:57
Saizou :
Albo tak jak pisze
5−latek
liczymy wyznacznik
| i j k |
det | x
1 y
1 z
1|
| x
2 y
2 z
2|
gdzie AB=[x
1,y
1,z
1] AC=[x
2,y
2,z
2]
Wyliczymy to i otrzymamy wektor [a,b,c]
| | 1 | |
pole obliczymy za pomocą wzoru P= |
| √a2+b2+c2 |
| | 2 | |
7 lip 23:03
Eta:
Zawsze najpierw sprawdzam co powie Pitagoras?

7 lip 23:10
Mila:
AB
→=[−3,−3,3]
AC
→=[1,−1,2]
=======
i j k
−3 −3 3
1 −1 2
=======
AB
→ x AC
→=−3i+9j+6k
======================
7 lip 23:12
Eta:
============ 
7 lip 23:13
Mila:
Zjadło mi cyfrę.
√9+81+36=√126
7 lip 23:13
Saizou :
Eta Pitagoras już chyba nic nie powie

7 lip 23:16
Eta:
Powiedział raz na zawsze ,że a
2+b
2= c
2 
7 lip 23:17
Saizou : Ja tam jestem przekonany że ufoludki wcześniej to wiedziały niż pan Pitagoras xd
7 lip 23:21
Mila:
Zawsze warto sprawdzić, czy Pitagorasek pasuje.

7 lip 23:26
ugabuga: Mila − to juz teraz sam nie wiem? bo mi wyszło √31,5
7 lip 23:48
ugabuga: Jeszcze takie zadanko
sprawdzić czy punkty A(2, 1 ,−1) B(−1, −2, 2) C(3, 0, 1) D(1, −4, 6) tworzą trapez
7 lip 23:57
Mila:
| | 1 | |
Włączyłeś |
| pod pierwiastek? |
| | 2 | |
To jest to samo.
| √63 | | √9*7 | | 3√7 | | 3*√7*√2 | | 3√14 | |
| = |
| = |
| = |
| = |
| |
| √2 | | √2 | | √2 | | 2 | | 2 | |
Ja liczyłam tak:
| 1 | | 1 | | 3√14 | |
| *√126= |
| *√9*14= |
| |
| 2 | | 2 | | 2 | |
7 lip 23:57
ugabuga: ale jest to taka sama liczba? czyli chyba wynik mi dobry wyszedł
8 lip 00:01
Mila:
Przecież to napisałam. Tak właśnie jest.
Jaką metodą liczyłeś?
Zadanie II.
Najpierw sprawdź, czy punkty A,B,C,D leżą w jednej płaszczyźnie, a potem czy jest para wektorów
równoległych.
8 lip 00:04
5-latek: kalkulator mowi ze to jet to samo
8 lip 00:05
ugabuga: taa ale wykładowca wpisał mi 2 i teraz nie wiem o co chodzi : (
rzutując trójkąt na płaszczyzny układu − liczyłem
8 lip 00:07
Mila:
Za co , za pierwsze zadanie?
8 lip 00:09
ugabuga: tak za pierwsze
8 lip 00:09
Mila:
Zadanie (1) albo tak jak Eta podała− obliczyć długości boków Δ i sprawdzić,
że to jest Δprostokątny, wtedy pole liczysz jak w gimnazjum,
albo tak jak pokazałam −za pomocą wyznacznika.
Zadanie (2)
Oblicz objętość czworościanu ABCD, jeśli jest równa 0, to znaczy, że punkty są
współpłaszczyznowe.
Sprawdzasz, czy są dwa boki równoległe ( wektorowo).
8 lip 00:16
Mila:
Dobranoc, jutro pisz.
8 lip 00:16
Mila:
2) AD→=[−1,−5,7]
−3 −3 3
1 −1 2
−1 −5 7
========
det(..)=0
||(AB→ x AC→) oAD→||=0⇔ punkty A,B,C, D są współpłaszczyznowe.
Sprawdź równoległość wektorów .
8 lip 16:13
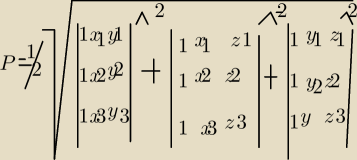 Ma by x1 x2 i x3 tez y1,y2y3 i to samo wspolrzedne z1 z2 z3
wyznaczniki pod pierwiastkiem do potęgi drugiej
Ma by x1 x2 i x3 tez y1,y2y3 i to samo wspolrzedne z1 z2 z3
wyznaczniki pod pierwiastkiem do potęgi drugiej





