zadanie nr 5 5-latek: mam do rozwiązania takie równanie logarytmiczne log₃ x+log₂(x+1)=2 Pisze ze tego równania nie rozwiążemy metoda elementarna Mam je doprowadzić do takiej postaci x^log₂(x+1)^log₃=10^{2log₃log₂} (nie wiem jak to zrobić i proszse o podanie dalszsego rozwiązania

5-latek: Przepraszam bardzo teraz zobaczyłem ze napisałem zle ma być taka postac x^log2(x+1)^log3= 10^2log3log2

5-latek: Teraz mi przyszla taka myśl żeby zmienić podstawy logarytmów

logx		log(x+1)
	+		=2 (czy dalej sprowadzić do wspolego mianownika (log3*log2 ?
log3		log2

ZKS: Obustronnie przemóż przez log3 * log2.

Mila: x>0 Zamiana podstaw logarytmów:

logx		log(x+1)
	+		=2 /*log(3)*log(2)
log(3)		log(2)

log(2)*logx+log(3)*log(x+1)=2log(3)*log(2) log(x^log(2))+log[(x+1)^log(3)]=log(9)*log(2) zwijamy logarytmy log[x^log(2)*(x+1)^log(3)]=log(9)*log(2)⇔ 10^{log(9)*log(2)}=[x^log(2)*(x+1)^log(3)]

5-latek: Dostane taka posatc log2*logx+log3*log(x+1)= 2log3*log2 tearz cos bym musial wylaczyc przed nawias po lwej stronie Tak?

5-latek: Witam jeszcze raz lilu Jeszcze nie za bardzo czaje tych mnozen logarytmów Możesz wyjasnic wiec dlaczego log(2)*logx= logx^log2 (tak po chłopsku

5-latek: Lila tez ladnie brzmi

ZKS: Z własności logarytmów clog_a(b) = log_a(b^c).

J: a*logx = logx^a

J: dla zabawy ...wyprowadz wzor: a*logx = logx^a

5-latek: Najpierw podziękowanie Podstawowy wzor . Po prostu nie skojarzyłem ze ze c czy a (czy jakakolwiek inna litera może być logarytmem . Teraz będę pamietal

5-latek: j jutro to zrobie

Mila: Na konkrecie: 2log(5)=log(5²)=log(25)

Eta:

	√37−1
Czy taką masz odpowiedź : x=
	2

5-latek: Witam i pozdrawiam Eta Niestety nie mam odpowiedzi do tego zadania

5-latek: Może taka być odpowiedz (chociaż tego nie lubie trzeba chyba będzie wpisac do wolframa

5-latek: x²+x−9=0 Δ=37 √Δ=√37

	−1−√37
x1=		<0 odpada
	2

	−1+√37		√37−1
x2=		=		>0
	2		2

WIedzialem ze to będzie hardcor to zadanie bo poprzednie przykłady tez były ciężkie Teoria i przykłady z książki J Slupecki , Z Garbaj T Sawicki . Arytmetyka i algebra (1969r

Eta: Ajjj faktycznie ... poplątałam zaraz skasuję

Mila: Wolfram nie zgadza się, ja jeszcze nie obliczyłam . To jest wariactwo.

ZKS:

	x		10log2
(		)log2 = (		)log3
	10log3		x + 1

Eta: Tak, tak ZKS teraz to zauważyłam

ZKS: Nie odświeżyłem przed wysłaniem i nie przeczytałem, że zauważyłaś już.

Eta: Hmm myślę jak go dokończyć .... takie zadanie , to sadyzm

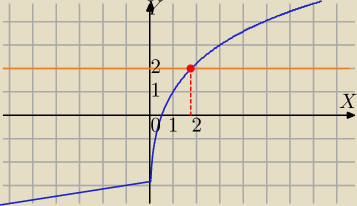
Mila: Rozwiąż równanie logarytmiczne. log₃ (x)+log₂(x+1)=2

5-latek: Milu Proponujesz rozwiązanie graficzne ?

ZKS: log₃(x) + log₂(x + 1) = 2 log₃(x) * log₃2 + log₃(x + 1) = 2log₃2 log₃(x^log₃2) + log₃(x + 1) = log₃4 x^log₃2 * (x + 1) = 4

	4
xlog32 =
	x + 1

Dokładnej wartości raczej się nie policzy, raczej trzeba byłoby szukać przybliżonej wartości z przecięcia się tych dwóch funkcji.

ZKS: Lub tak 2^log₃(x) * (x + 1) = 2² x + 1 = 2^{2 − log₃(x)}.

5-latek: jeśli by CI nie sprawilo dużego kłopotu to proszse rozpisz dokładnie ta druga linijke

5-latek: Chodzi o post z 23:52

Mila: Dobranoc, 5−latek, nie wstaniesz jutro do pracy.

Michcio: Czemu 5−latek rozwiązujesz w wakacje zadania ? Podobno masz 50 lat (tak gdzieś tu wyczytałem)

5-latek: Milu do końca tygodnia mam urlop (w sobote zadzwonili z pracy

ZKS: log₃(x) + log₂(x + 1) = 2

	log3(x + 1)
log3(x) +		= 2
	log32

log₃2 * log₃(x) + log₃(x + 1) = 2log₃2

5-latek: Rozumiem dziekuje dobranoc

ZKS: Dobranoc.

Lukas: Dobranoc.