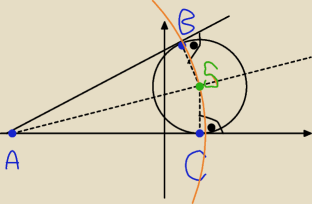
GEOMETRIA ANALITYCZNA - równanie stycznej zmiotka: Okrąg przedstawiony na rysunku jest styczny do osi OX w punkcie (2,0), a prosta k przechodzi przez punkt A=(−6,0) i jest styczna do okręgu w punkcie B. a) Jaką długość ma odcinek AB? b) Znajdź równanie stycznej k wiedząc, że punkt A znajduje się w odległości 6√2 od środka okręgu. A=(−6,0) B= ? C=(2,0) S=(2,?) , z IASI=6√2 ⇔ √(2+6)² + (0−r)² ⇔...⇒ r=2√2 IASI=6√2 a) IABI = IACI ⇔ ... ⇔ IABI = 8 b) k:y= ax + b A∊k ⇔ 0= −6x + b ⇔ b = 6x k:y= ax + 6x Proszę o jak najwięcej sposobów rozwiązań. Powinno wyjść 4√2x − 7y + 24√2 = 0

zmiotka: k:y= ax + 6x a= tgα

zmiotka: tfu, b = 6a równanie ogólne k: ax − y + 6a Z tego można skorzystać tak, że d(S;k)=2√2⇔ I2a −2√2 + 6aI : √a² + 1 = 2√2 ...?

Mila: Odległość środka okręgu od stycznej jest równa 2√2. k: y=ax+b 0=−6a+b b=6a k: y=ax+6a⇔ ax−y+6a=0 S=(2,2√2)

	|2a−2√2+6a|
d(S,k)=		=2√2⇔
	√a2+1

|8a−2√2|=2√2*√a²+1 /² 64a²−32√2a+8=8*(a²+1) 56a²−32√2a=0 a*(56a−32√2)=0 a=0 ,stąd y=0 jedna styczna − oś OX lub

	32√2
a=
	56

	4√2
a=
	7

	4√2		6*4√2
k:		x−y+		=0 /*7
	7		7

k: 4√2x−7y+24√2=0 ================

zmiotka: Należy dodać: zał.a>0 a jak obliczyć to korzystając z własności, że tgα=a ? undefined

Kacper: Liczysz tg podwojonego kąta i z tego korzystasz