trójkąt uff jak gorąco !: W trójkącie ostrokątnym ABC , na bokach AC i BC zbudowano na zewnątrz prostokąty ACMN i BCKL o jednakowych polach. Wiedząc,że P jest środkiem odcinka MK i punkt O jest środkiem okręgu opisanego na trójkącie ABC wykaż,że punkty O , C, P są współliniowe.

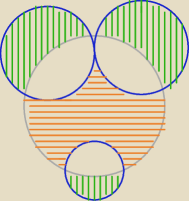
uff jak gorąco !: Zad.2 Dane są koła ( jak na rys.) o promieniach długości: 2,4,4,6 Wykaż ,że pola ( zielone i rude są równe

5-latek: ale upał

uff jak gorąco !:

henrys: Piękne...

Mila: Czy środki małych okręgów leżą na najdłuższym okręgu?

henrys: Rozumiem, że małe kółka nie mogą na siebie zachodzić

uff jak gorąco !: Odp : @ Mili .... nie

uff jak gorąco !:

PW: Ruszanie małymi kółkami w górę lub w dół powoduje wzrost lub ubytek zielonych pól, o tyle samo rośnie lub maleje czerwone pole. Zacząć od takiego położenia małych kół, że są styczne zewnętrznie z dużym kołem. Wtedy czerwone pole to π6² = 36π, a zielone pola to 2π4² + π2² = 36π. Na razie się zgadza − czerwone i suma zielonych pól są równe. Wystarczy udowodnić prawdziwość pierwszego zdania.

uff jak gorąco !: Białe pola oznaczam P₁, P₁, P₂ zatem polezielone jest równe: 2*16π+4π −(2P₁+P₂)= 36π−(2p₁+P₂) pole rude jest równe : 36π− (2P₁+P₂) wniosek : Pzielone= Prude

bezendu:

uff jak gorąco !: ?

bezendu: To środkowe

uff jak gorąco !:

uff jak gorąco !: Zadanie 1/ ..... wciąż czeka ... Kto chętny?

bezendu: Pisz do Ety jak wpadnie to pewnie zrobi

uff jak gorąco !: A potrafi?

Mila: Eta pisze do Ety?

bezendu: To zdolna bestia

uff jak gorąco !: Pod koniec tygodnia jadę na 2 tyg. do Łeby

bezendu:

Mila: A potem do Nałęczowa.

bezendu: Do Sopotu na molo albo do Gdańska/Oliwy do zoo. Polecam

uff jak gorąco !: W sierpniu jadę do Iwonicza Zdroju ... polecam

bezendu: A potem Eta z gór przynosi zadania dla gadów które piszą maturę

Hajtowy: HAHAHAH XD

uff jak gorąco !: A zad. 1 .... czeka

uff jak gorąco !: A co na to Kacper

bezendu: Też mu gorąco w tali upał

uff jak gorąco !: Może też podlega pod art. 216 kk ?

Daras: To już musisz zapytać twojego guru ponieważ ściganie odbywa się z oskarżenia prywatnego.

Mariusz: Ładny rysunek Jest do niego jakieś zadanie

Mariusz:

Damian1996: W pierwszym zadaniu próbowałbym tak: Punkty P oraz O leżą na jednej prostej. Aby wykazać, że punkt C, również leży na tej prostej, musimy udowodnić, że ∡OCP jest półpełny. Skoro ACMN jest prostokątem, to ∡ACM=90 stopni. Zauważmy, że ΔAOC jest równoramienny, więc ∡OCA=∡CAO=α. Kąty OCA i PCK są wierzchołkowe, czyli oba mają miarę α. Kąty BCO i MCP również są wierzchołkowe, więc mają równe miary. A ponieważ ∡BCO+∡MCP=180−2α, to ∡MCP=90−α. Czyli ∡OCP=90+α+(90−α)=180 stopni, cnw. Poprawcie mnie, jeśli strzeliłem jakiegoś blefa

anaisy: Damian1996, kąty OCA i PSK są wierzchołkowe tylko wtedy, gdy P, C, O leżą na jednej prostej. A to dopiero chcemy udowodnić.

Damian1996: Tak, tak.. Za łatwe by to było W dodatku z pominięciem dwóch (zapewne istotnych) danych z treści zadania

anaisy: Oznaczmy AC=a, BC=b, MC=bx, wtedy z założeń zadania mamy CK=ax. Niech teraz R będzie punktem po przeciwnej stronie MK niż C, takim, że RM=bk i RK=ak. Wtedy trójkąty ACB i KRM są podobne. Ponadto mamy ∡MCK+∡MRK=∡MCK+∡ACB=180[deg]. Stąd wniosek, że punkty R, K, C, M leżą na jednym okręgu. Ponadto RK*MC=CK*MR, czyli RC jest symedianą w trójkacie MCK. Stąd ∡DCM=∡RCK, a z tw. o kątach opartych na tym samym łuku (w (RKCM)) ∡RCK=∡RMK, zatem z podobieństwa RKM i ABC mamy ∡DCM=∡CBA. Ponieważ ABC jest ostrokątny, więc ∡ACO=90[deg]−∡CBA, skąd ∡ACO+∡DCM=90[deg], czyli D, C, O są współliniowe.

Eta: Szkoda,że bez rysunku ( rysunek to podstawa do tego typu zadań

bezendu: Rys: 5 lip 2015 23:59

Eta:

anaisy: Eta, przecież opisałam dokładnie, jak konstruujemy dane punkty. Jeżeli ktoś będzie zainteresowany tym zadaniem, z pewnością narysuje sobie rysunek.

Eta: W nagrodę ...

anaisy:

Eta: Kolejne zadanie z planimetrii,która sprawia uczniom najwięcej kłopotów Zad.3 Przekątne AC i BD czworokąta wypukłego ABCD przecinają się w punkcie S. Punkt E jest środkiem boku DC. Prosta poprowadzona przez punkty E i S przecina bok AB w punkcie F.

	P(ΔASD)		|AF|
Wykaż ,że		=
	P(ΔBSC)		|FB|

P.S . Przedstawić dowód wraz z rysunkiem Powodzenia

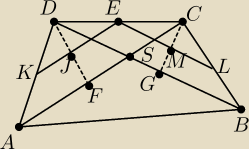
anaisy: Niech K i L będą środkami DA i CB a punkty F i G rzutami prostokątnymi D na AC i C na BD oraz J=KE∩DF i M=EL∩CG.

	[ADS]		[ASE]
Lemat 1.:		=
	[BCS]		[BSE]

Dowód: Zauważmy, że trójkąty ASE i ADS mają jeden wspólny bok oraz wysokość trójkąta ADS op. na ten bok jest dwa razy dłuższa od wysokości ASE op. na ten bok (z definicji punktu K). Stąd

	[ASE]		1		[ESB]		1
		=		. Analogicznie mamy		=		. Stąd
	[ADS]		2		[SCB]		2

	[ASE]		[ESB]		[ADS]		[ASE]
		=		, czyli również		=		.
	[ADS]		[SCB]		[BCS]		[BSE]

	[ASE]		[ASF]
Lemat 2.:		=		.
	[BSE]		[BSF]

Dowód. Niech a, b oznaczają odpowiednio odległości punktów A, B od EF. Wtedy:

	ES*a
[ASE]=
	2

	ES*b
[ESB]=
	2

	SF*a
[ASF]=
	2

	SF*b
[BSF]=
	2

Stąd łatwo wynika dowodzona równość

	[ASF]		AF
Lemat 3.:		=		.
	[BSF]		BF

Dowód: Niech c oznacza odległość punktu S od AB. Wtedy

	[ASF]		AF*c*1/2		AF
		=		=		.
	[SFB]		FB*c*1/2		BF

Łącząc te trzy lematy uzyskujemy tezę.

anaisy: Zrobiła się mała kolizja oznaczeń, ale łatwo to naprawić: Punkt F zaznaczony na rysunku jest wykorzystywany tylko w lemacie 1.

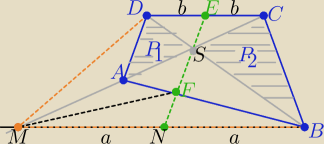
Eta: Podaję inny sposób:

	P(ΔASD)		|AF|
Teza:		=
	P(ΔBSC)		|FB|

Wykreślam trapez MBCD ( jak na rys.) Z podobieństwa trójkątów MBS i DCS i z treści zadania |DE|=|EC| ⇒ |MN|=|NB| SN jest środkową trójkątów MBS i MBF⇒ P(ΔMNS)=P(ΔBNS) i P(ΔMNF)=P(ΔBNF) to P(ΔMFS)=P(ΔBFS) z własności w trapezie ⇒ P(ΔMSD)=P(ΔBSC) zatem:

P(ΔASD)		PΔASD)		|AS|		P(ΔAFS)
	=		=		=		=
P(ΔBSC)		P(ΔMSD)		|MS|		P(ΔMFS)

	P(ΔAFS)		|AF|
=		=
	P(ΔBFS)		|FB|

c.n.w

Mila: Trapez dobry na wszystko

Eta: Szkoda ,że na upał nie pomaga

Metis:

Eta: Uffff jak gorąco

Eta: No i .... anaisy zamilkła?