tryg bimbam:

	π
dla jakich x∊(0;		) są spełnione nierówności
	2

	3tgx − ctgx
−1<		< 0
	2

3tgx − ctgx		3tg2x − 1		π
	=		i dla x∊(0;		) : tgx>0
2		2tgx		2

więc

	3tg2x − 1
−1<		< 0
	2tgx

3tg²x − 1 > − 2tgx i 3tg²x − 1 < 0 3tg²x + 2tgx − 1 > 0 i 3tg²x − 1 < 0 jeśli t=tgx, to ad1/ 3t²+2t−1>0

	1		1
t∊(−∞;−1) u (		; ∞) jak obliczyć tgx=
	3		3

ad2/ 3t²−1<0

	√3		√3
t∊(−		;		)
	3		3

	π		π
jeśli x∊(0;		) , to 0<x<
	2		6

	π		1
Jak uzyskać odpowiedź z książki, tj. α<x<		, gdzie tgα=
	6		3

Mila:

	1		√3		π
tgx>		i tgx<		i tgx>0 z założenia (x∊(0,		)
	3		3		2

1		√3
	<
3		3

	π
tgx jest funkcją rosnącą stąd α<		⇔
	6

	π		1		1
α<x<		, gdzie tgα=		⇔α=arctg(		) nie liczysz tego, chyba że jest takie
	6		3		3

polecenie, to odczytujesz w tablicach.

x&y:

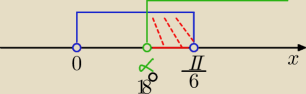
	1
tgx=		⇒ x≈18o
	3

	1
Odp: x∊( α, π6) gdzie tgα=
	3

bimbam: tgx jest f. rosnącą, więc znak nierówności się nie zmienia − tak jak w logarytmach Jeśli tak, to rozumiem. Dzięki Mila i x&y