tryg bimbam: sin²⁹3x−cos¹⁷10x=2 tutaj próbowałem rozwiązać to w ten sposób sin czegokolwiek to maksymalnie 1, a minimalnie (−1) cos czegokolwiek to maksymalnie 1, a minimalnie (−1) więc jedyna możliwość to a−b=2 gdzie a=+1 i a=sin²⁹3x ⇒ sin²⁹3x = +1 b=−1 i b=cos¹⁷10x ⇒ cos¹⁷10x=−1 czyli 1−(−1)=2 sin²⁹3x = +1 sin3x = +1

	π		2kπ
x=		+
	6		3

cos¹⁷10x=−1 cos10x=−1

	π		kπ
x=		+
	10		5

	3π
niestety prawidłowa odpowiedź to		+ 2kπ
	2

henrys:

	π		2kπ		π		mπ
Może spróbuj tak, x=		+		=		+
	6		3		10		5

henrys: Znajdź zależność między k i m

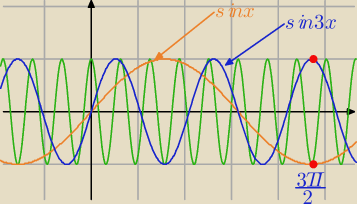
Mila: Sprawdź w przedziale <0,2π> dla jakiego argumentu (wszystkie możliwości) sin(3x)=1 Następnie szukaj wśród tych argumentów takiego, aby spełnione było równanie cos(10x)=−1

Mila: Z jakiego zbioru korzystasz?

henrys: Fajne zadania

bimbam: ...musiałem zrobić sobie przerwę dziękuję Wam za pomoc Korzystam z "Matematyka dla maturzystów" Wacław Leksiński, Bohdan Macukow, Wojciech Żakowski, WNT, Warszawa 1994

Mila: