Jak sobie poradzić z taką nierównością? Rowerek: √10+x<^13+x₄ Niestety nie rozumiem do końca tych przykładów Czy jest ktoś w stanie mi pomóc?

Mila: 10+x≥0⇔x≥−10 dla x≥−10 prawa strona jest dodatnia, możesz obie strony nierówności podnieść do kwadratu.

Rowerek: x należy do przedziału ≤−10, ∞) 10+x<^169+26x+x2₁₆ 0<x²+10x+9 Δ=64 x1=−9 x2=−1 Jak to interpretować?

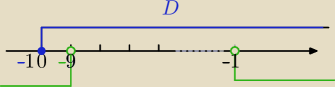
Mila: x∊<−10,−9)∪(−1,∞)

Rowerek: Aa, trochę mi się rozjaśniło. Jeszcze jeden przykład, trochę trudniejszy: √(x+7)(x+1)>x+3 x∊(−∞, −7> oraz <−1, ∞)

Mila: 1) Dla x∊(−∞, −7> lewa strona nierówności ma wartość nieujemną a prawa strona jest ujemna, zatem nierówność jest spełniona dla każdego x z tego przedziału. 2) dla <−1, ∞) obie strony nierówności są nieujemne, możesz obustronnie podnieść do kwadratu. Rozwiązuj.

Rowerek: √(x+7)(x+1)>x+3 (x+7)(x+1)>x²+6x+9 x²+8x+7>x²+6x+9 2x>2 x>1 x∊(1, ∞) i sumując x∊(−∞, −7> i (1, ∞)

Rowerek: Ojej, dzięki tobie te nierówności stały się niesamowicie proste Postaram się rozwiązać resztę zadań samodzielnie. Dziękuję bardzo za pomoc

Mila: