szereg Saris: Hej.

	n2+1
∑n=1∞ ln
	n2

Szereg jest zbieżny. Da się to jakoś szybko wykazać bez używania kryt. całkowego? Jeśli tak jakim kryterium i ewentualnie jaki drugi ciąg. Z góry dziękuje za podpowiedź.

Saris: chyba strona miała jakieś opóźnienie, bo wyslałem temat, jak odświeżyłam to się nie pojawił i napisałem kolejny.

ICSP: Kryterium Cauchy'ego powinno zadziałać.

Saris: Z Cauchey'ego dostanę granicę 1, tak samo z D'Alemberta.

ICSP: Pokaż

Saris: Dobra to jednak to nie będzie takie proste, ta granica jest dość dziwna. W sumie jestem w kropce.

ICSP:

	1
lim ln(1 +		)1/n = ln elim 1/n3 = ln eo = ln(1) = 0 <1
	n2

kyrtap: ta granica nie była dziwna

Saris: myslalem ze jak mi wyszlo 0 to bylo zle, no niby nie byla. Dziekuje.

john2:

	1		1
mogę dopytać, czemu tam jest ln(1 +		)1/n a nie cały [ln(1 +		)]1/n ?
	n2		n2

Saris: żeby wrzucić tam eksponencjał (nie wiem czy mzona tak to nazwac).

john2: Ahaa..właśnie zaczynam zabawę z szeregami i widzę, że zabawa będzie dość... długa.

Saris: Taki przykład:

	1
∑n=1
	n2 ln2n

kryt. por.

1		1
	<=		(zb.) ⇔ nasz szereg jest zbieżny.
n2 ln2n		n2

I inny:

	1		1
∑n=1 sin		cos
	n		n

Jakiś pomysł na to?

Saris: Dobra, już wymyśliłem kryt. ilorazowe do tego

Saris:

	1
∑
	n(√n−1−√n)

Ma ktoś pomysł na taki szereg?

Godzio: Pomnóżmy licznik i mianownik przez √n − 1 + √n

	√n − 1 + √n
... = − ∑
	n

	√n − 1 + √n
Rozważmy szereg ∑
	n

√n − 1 + √n		√n		1
	≥		=
n		n		√n

	1		√n − 1 + √n
szereg ∑		jest rozbieżny, z kryterium porównawczego ∑		również
	√n		n

rozbieżny, a zatem nasz szereg jest także rozbieżny

Saris:

	3−(−1)n
1. ∑ (−1)n+1 *
	2n

limes z tego dązy do 0. bezwzględne wyrazy twarzą ciąg malejący, więc kryt. Leibnitza jest spełnione i ten szereg powinien być zbieżny (bezwględnie nie jest), ale w odpowiedziach piszę, że jest rozbieżny. Czemu?

	1
2. ∑ sin(n+		)π
	n

3. ∑ sin(naⁿ)

	1
4. ∑
	3√n

Pomoże ktoś, bo te 3 ostatnie to nie wiem jak zacząć.

Saris: Dzięki Godzio, już zrobiłem wcześniej kryt. ilorazowym.

Saris: znaczy w 3, a<|1|, żeby WK zachodził.

Godzio: Obawiam się, że 1 nie jest malejąca.

	4
a1 =
	2

	2
a2 =
	4

	4
a3 =
	5

Skacze, ale nie jest malejący

Godzio:

	3(−1)n+1 + 1
Wymnóżmy :
	2n

Dla n parzystych mamy:

−3 + 1		−2		1
	=		= −
2n		2n		n

Dla n nieparzystych mamy

3 + 1		2
	=
2n		n

	3(−1)n+1 + 1		1		2
∑		= ∑n=1∞(−		+		) =
	2n		2n		2n−1

	−2n + 1 + 4n		2n + 1
∑n=1∞(		= ∑n=1∞
	2n(2n − 1)		2n(2n − 1)

	1
A to już chyba widać, z kryterium ilorazowego, że jest to szereg rozbieżny (bn =		)
	n

Saris: Hm, hm. Bo ja się kierowałem tym kryterium Leibnitza, które mówi, że jeśli mamy do czynienia z szeregiem przemiennym (mamy), jest spełniony WK na zbieżność (jest) oraz bewzględne wyrazy tego szeregu twarzą ciąg malejący(generalnie to nierosnący) albo równoważnie |a_n+1|<=|a_n| to szereg taki jest zbieżny.

	3		(−1)n		3
|...|= | (−1)n+1 *		− (−1)n+1 *		| = | (−1)n+1 *		| − |
	2n		2n		2n

	(−1)n		3		1
(−1)n+1 *		| =		−		.
	2n		2n		2n

Gdzie ja tu błąd robię? Teraz wstawiałem po kolei wyrazy i patrzyłem jak się zmieniają bezwzględne wyrazy tego ciągu.

Saris: tam na końcu definicji brakuje od pewnego N<n.

Godzio: A gdzie w kryterium masz taką własność? Pierwszy raz widzę informację o bezwzględnych wyrazach.

b.: jeszcze do początkowego zadania: > Saris: Z Cauchey'ego dostanę granicę 1, tak samo z D'Alemberta. 3 lip 16:58 Masz rację, żadno z nich nie zadziała. Rozwiązanie ICSP (3 lip, 17:25) jest błędne.

	n2+1		1
Trochę nieformalnie, ln(1+x)≈x dla x≈0, więc ln		≈		, skąd kryteria C. i
	n2		n2

d'A. nie działają. Można np. użyć porównawczego: ponieważ ln(1+x) <= x (z wklęsłości logarytmu), więc

	n2+1		1
0 <= ln		<=		.
	n2		n2

@Saris, 21:52: błąd robisz w drugiej równości, nie jest na ogół prawdą, że |x−y|=|x|−|y|.

b.: Poza tym, Godzio Ci pokazał, że |a₃| = 4/5 > 1/2 = |a₂|, więc żeby znaleźć błąd w Twoim rachunku, wystarczyło podstawić n=2, n=3 i zobaczyć, co się nie zgadza.

Saris: No widzę już, co źle zrobiłem. Dzięki. Jest jakaś metoda, na znajdowanie sumy szeregów typu: 1−1/2+1/3−1/4+... w których właśnie nic się na pierwszy rzut oka nie skraca?

Saris: Znaczy nie chodzi mi o sumę tylko wzór sumowanego ciągu.

Saizou :

	1
a coś takiego ∑(−1)n+1		sumowanie do n=1 do ∞
	n

b.: = ln 2, tutaj metoda to rozwinięcie funkcji ln(1+x) w szereg Maclaurina, ale ogólnej metody raczej nie ma

Saris: Ehh patrzyłem na teorię tych wszystkich zbieżności w szeregach funkcyjnych, obszarów itd. i jest to dla mnie dziwne. Jak się takiej góry teorii nauczyć... Już całe całki wielokrotne były prostsze. Dzisiaj zrobiłem koło 60 tych zbieżności, żeby się wprawić w te wszystkie kryteria, a tu widzę, że to wierzchołek góry lodowej.

b.: Na razie pisałeś tylko zwykłe szeregi liczbowe, i słusznie, naucz się najpierw dobrze tego, zanim przejdziesz do szeregów funkcyjnych.

Saris: Jesli mamy jakies typowe zadanie z wykazywaniem zbieznosci jednostajnej i bezwglednej, to dzieki kryt. Weierstrassa wykażemy zb. jednostajną, a co z bezwględną? w tw. mamy: |f_n(x)|<=an. To zbieżnośc bezwględną, wykażemy przy okazji? Pytam, ponieważ samo kryt. nie mówi o zb. bezwględnej.

Saris: Rozwiń w szereg Maclaurina funkcję f(x)=arctg(x²). Dla jakich x otrzymany szereg jest zbieżny? Dla jakich x wartość f(x) jest równa sumie otrzymanego szeregu? f(x)=arctg(x²)

	2x
f'(x)=		= | a0=x, q=−x4, q∊(−1;1) | = 2∑ x*(−x4n) = 2∑ (−1)4n*x4n+1 = 2∑
	1+x4

x⁴ⁿ⁺¹

	x4n+1
f(x)=∫f'(x)dx= 3∑		+C
	4n+2

f(0)=0 C=0

	x4n+1
f(x)=∫f'(x)dx= 2∑		∀x∊(−1;1)
	4n+2

dla x=1:

	1		1		1
f(−1)= 2∑		kr. ilor. gdzie an=		bn=		, lim n−>∞
	4n+2		4n+2		n

	an		1
		=		∊ (0; ∞) ⋀ bn rozb. ⇒ an rozb.
	bn		4

Zatem w x=1 szereg rozb. To samo w x=−1

	x4n+1
Zatem f(x)= 2∑		jest zbieżny ∀x∊(−1;1)
	4n+2

∑ − ∑ od n=0 do ∞ 1. Czy dobrze? 2. Jak odpowiedzieć na ostatnie pytanie? Wyznaczyć sumę i sprawdzić kiedy S(x)=f(x)? Czy tak czy może inaczej? Dzięki za pomoc z góry.

Mila:

	1		1		1		1		xn.
ln(1+x)=x−		x2+		x3−		x4+		x5+..+(−1)n+1		.....
	2		3		4		5		n

dla x=1 S=ln(2)

b.: @22:24: jest drobna pomyłka w wierszu z f'(x)=..., powinno być f'(x) = ... =2 ∑ x*(−x⁴)ⁿ, więc potem będzie dodatkowy czynnik (−1)ⁿ lepiej pisać np. f(x) = ∫₀^x f'(t), bo twierdzenie o całkowaniu szeregów dotyczy całek oznaczonych ze względu na brakujący czynnik (−1)ⁿ szereg będzie zbieżny na końcach Jeśli chodzi o równość, to dla x∊(−1,1) jest ona jasna (mamy równość z szeregiem geometrycznym, odcałkowujemy, itd.). Natomiast równość na końcach wynika na przykład z ciągłości sumy szeregu potęgowego (zob. tw. Abela). @23:18: Tutaj też standardowo potrzeba np. tw. Abela, bo początkowo równość jest dla x∊(−1,1) (przez odcałkowanie szeregu geometrycznego dla 1/(1+x) ). Choć to oczywiście zależy od tego, co uważamy za punkt wyjścia, jeśli przyjmujemy, że znamy rozwinięcie ln(1+x) i wiemy, że jest ono słuszne dla x∊(−1,1], to oczywiście tak jak jest jest ok.

Saris: Ok. Głupi błąd. Dzięki. Popatrzyłbyś jeszcze na tą teor. kwestię z 20:58?

b.: Saris: Jesli mamy jakies typowe zadanie z wykazywaniem zbieznosci jednostajnej i bezwglednej, to dzieki kryt. Weierstrassa wykażemy zb. jednostajną, a co z bezwględną? w tw. mamy: |f_n(x)|<=a_n. To zbieżnośc bezwględną, wykażemy przy okazji? Zgadza się, bo dla szeregu ∑|f_n(x)| mamy dokładnie takie samo oszacowanie | |f_n(x)| | = |f_n(x)| <= a_n i kryterium W. też działa.

Saris:

	xn
Zbadać zbieżność jedn. szeregu funkcyjnego od n=1 do ∞ ∑		na przedziale [1;∞).
	1+n5x2

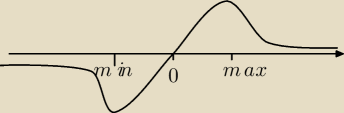
Policzę granicę na końcach przedziałów i znajdę ekstremum. [Znaczy funkcja dana w x=1, więc granicę wystarczy w ∞, a x=1 po prostu wyliczyć wartość (dobrze?)] Wyjdą 2 i jedno będzie minimum i jedno maximum, ale jak ocenić czy to moje ekstremum max mieści się w zakresie i czy przypadkiem na takim przedziale nie powinien brać f(1) jako maksimum (które też jest zbieżne i podchodzi pod Weiestrassa). Jak dla x>max funkcja maleje, więc jeśli 1>max to f(1) jest ekstremum. Sytuacji wygląda jak na rysunku gdzie:

	1
max =
	n5/2

	1
min = −
	n5/2

	n
f(1) =
	1+n5

	1
f(max) =
	2n3/2

Mam nadzieję, że ktoś wie o co mi tutaj chodzi . Pomocy.

Saizou : Łatwiej zbadać czy jest on bezwzględnie zbieżny

	xn		|nx|		|nx|		n		1
|		|=		= ≤		=		=		a
	1+n5x2		|1+n5x2|		2|n5/2x|		2n5/2		2n3/2

taki szereg jest zbieżny, wiec na mocy kryterium Weierstrass, szukany szereg jest zbieżny (skorzystam z nierówności a²+b²≥2|ab|)

henrys: a nie możesz tak?

nx		nx2		1
	≤		=
1+n5x2		n5x2		n4

b.: @14:13: po to się szuka ekstremów lokalnych i wartości na końcach, żeby znaleźć sup_x f_n(x).

	n		1
W naszym przypadku jest ono równe max{		,		} (nie sprawdzałem
	1+n5		2n3/2

	n		1		1
rachunków), a ponieważ		<		<=		, więc dostajemy, że
	1+n5		n4		n3/2

	1
0 < fn(x) <=
	n3/2

stąd zbieżność jednostajna. Ale jak widać z następnych postów, czasami łatwiej zgrubnie oszacować niż liczyć ekstrema.