przeciwdziedzina john2: Jaka jest przeciwdziedzina funkcji f(x) = x² ? Czy jest dowolny zbiór zawierający zbiór [0,+∞) ? Czyli na przykład mogę sobie wymyślić, że jej przeciwdziedziną jest zbiór (−50,+∞) ? Czym właściwie wtedy taka funkcja będzie się różnić od funkcji z przeciwdziedziną [0, +∞), czyli pokrywającą się ze zbiorem wartości? Bo, jak rozumiem, wykres będzie identyczny.

J: nie dowolny zbiór, tylko: Z_w = [0,+∞) , to jak możesz napisać: (−50,+∞) ?

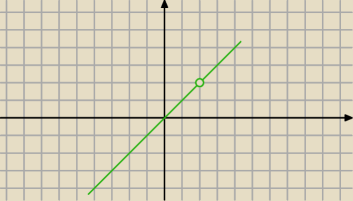
J: Co jest przeciwdziedziną tej funkcji ?

john2: Hmm. Zbiorem wartości tutaj jest R\{2}, a przeciwdziedziną...albo R albo R\{2}, nie wiem.

J: tak mówi "wiki": przeciwdziedzinę nazywa się czasem zbiorem wartości funkcji, chociaż właściwszym stwierdzeniem jest że: przeciwdziedzina zawiera zbiór wartości funkcji czyli Twoje pierwsze stwierdzenie było prawdziwe .. ja osobiście utożsamiam przeciwdziedzinę ze zbiorem wartości ( ale może niesłusznie)

john2: No właśnie. Tylko teraz coś takiego znalazłem https://pl.wikipedia.org/wiki/Funkcja_kwadratowa pod "Własności i przebieg" na dole. f: R −> R Wychodzi na to, że przeciwdziedziną jest R, więc w końcu chyba nie jest dowolnym zbiorem zawierającym zbiór R₊. Gubię się w tym.

J: pojęcie przeciwdziedziny jest pojęciem szerszym , z tego co pokazłeś wynika, że funkcja f(x) =ax² + bx + c , to funkcja: f: R → R , której przeciwdziedziną jest zbiór R, a zbiory wartości są podzbiorami R, zaleznymi od a

john2: To ma sens. Nie znając a, może okazać się, że funkcji przyjmuje wartości ujemne. To pasuje do ogólnej postaci funkcji kwadratowej. Ale teraz ciekawe, co jeśli znamy a. Czyli np. f(x) = x² Czyżby tu przeciwdziedzina była równa zbiorowi wartości..

J: no, wedle tego co znaleźliśmy wynika, że nadal przeciwdziedziną jest R , a zbiorem wartości jej podzbiór: [0,+∞)

henrys: ale jak chyba napiszesz f:R→R₊u{0} to PD będzie równa zbiorowi ZW

john2: Teraz patrzę tu: https://pl.wikipedia.org/wiki/Funkcja_%22na%22 pod Definicja − Uwaga "Należy pamiętać, że to wybór przeciwdziedziny decyduje o surjektywności lub jej braku" Czyli chyba jednak to jest kwestia wyboru.

john2: Generalnie moje pytanie się sprowadza do tego.. Czy mogę sobie napisać np. f: R → (−50,+∞) f(x) = x² i czy taka funkcja się wizualnie czymś różni od takiej: f: R → [0,+∞) f(x) = x²

J: niczym ... wybrałeś dwie przeciwdziedziny , ale zbiór wartości jest ten sam .. oczywiście w tej sytuacji pierwsza funkcja nie jest suriekcją

henrys: a znacie jakieś funkcje, których ZW nie da się określić, a jedynie podać Zbiór zawierający te wartości?

henrys: Dla takich funkcji jak napisałeś możesz od razu określić PD=ZW. Weźmy np. f: PxP→Z, gdzie P jest zbiorem liczb pierwszych,taką, że f(p₁,p₂)=p₁+p₂. Ja nie znam jej ZW. Chyba mogę tak określić funkcje ?

john2: henrys raczej nie nadążam za Twoim tokiem rozumowania, ja dopiero "jestem w przedszkolu" jeśli idzie o matematykę. Chodzi o to, że nie mogę wybrać sobie przeciwdziedziny, nie znając zbioru wartości? Ale jak znam, to mogę?

henrys: Chyba dlatego w przykładach szkolnych przeciwdziedzina jest utożsamiana ze ZW.

henrys: Chyba dlatego w przykładach szkolnych przeciwdziedzina jest utożsamiana ze ZW.

henrys: Przeciwdziedzinę możesz wybrać ale nie zawsze potrafisz określić jej ZW

henrys: Musisz podać dziedzinę i przeciwdziedzinę.

henrys: Ja nie wiem czy do przedszkola się kwalifikuję

john2: Ok. Muszę jeszcze o tym porozmyślać. Dziękuję za odpowiedzi.

Janek191: f − funkcja rzeczywista f : ℛ → ℛ oznacza tylko tyle,że argumenty należą do ℛ ( x ∊ ℛ ) oraz wartości funkcji należą do ℛ ( y = f(x) ∊ ℛ ) Zawsze ZW ⊂ ℛ lub ZW = ℛ ZW − zbiór wartości funkcji ?