dane sa punkty rownolegloboku wyznacz pkt d betita: punkty A (1,1) B (2,3) c(−4,−5) sa kolejnymi wierzcholkami rownolegloboku ABCD wyznacz a) wspołrzedne punktu d b) pole równolegloboku c) obwod d) dlugosc przekatnych prosze bardzo o pomoc

AROB: pomogę

betita:

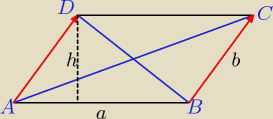
AROB: a) Współrzędne punktu D najprościej obliczamy z równości wektorów, np. wektor AD = wektor BC wektor AD = [x_D − x_A, y_D − y_A] = [x_D − 1, y_D − 1] wektor BC = [x_c − x_B, y_C − y_B] = [−4 −2, −5 −3] = [−6, −8] AD = BC ⇔ x_D − 1 = −6 y_D − 1 = −8 x_D = −5 y_D = −7 , czyli D(−5, −7) b) P = a*h h − to odległość punktu D od prostej AB Wyznaczamy równanie prostej AB:

	yB − yA
y − yA =		(x − xA)
	xB − xA

	3 − 1
y − 1 =		(x − 1)
	2 − 1

y = 2(x − 1) + 1 ⇒ y = 2x − 1 ⇔ 2x − y − 1 = 0

	IAxD + ByD + CI		I2*(−5)−1*(−7)−1I		I−4I
d =		=		=		=
	√A2 + B2		√4 + 1		√5

	4√5
	5

	4√5
Czyli h =		.
	5

a = IABI = √(x_B−x_A)² + (y_B−y_A)² = √(2−1)² + (3−1)² = √5 P = ah = √5 * U{4√5{5} = 4 [j²] Zaraz poślę dokończenie.

AROB: c) ob = 2a + 2b, a = √5 b = IBCI = √(x_C −x_B)² + (y_C−y_B)² = √(−4−2)² + (−5−3)² = √36+64 = 10 ob = 2*√5 + 2*10 = 2(√5 + 10) [j] d) przekątne: IACI = √(x_C−x_A)² + (y_C−y_A)² = √(−4−1)² + (−5−1)² = √25+36 = √61 IBDI = √(x_D−x_B)² + (y_D−y_B)² = √(−5−2)² + (−7−3)² = √49 +100 = √149

betita: dziekuje ci bardzo

AROB:

betita: naprawde jestem ci wdzieczna

AROB: Cieszę się. Dobranoc! Dobranoc Eto i Bogdanie .

Bogdan: Ja też już idę spać. Dobranoc

B: super, dziękuję

basia: Wyznacz wspolzedne punktuA bedocego obrazem punktuA=(−3,4) w symertri wzgledem punktu S=(2,−1)

basia:

blabla:

xA+xB		yA+yB
	=xS i		= yS
2		2

to x_B=2x_S−x_A i y_B=2y_S−y_A x_B=3+8 i y_B=10−5 B(11,5) =======

blabla: @ ICSP dlaczego skasowałeś wpis ? I właśnie przez takie zachowania ... mnie podejrzewają o kasowanie wpisu ! !

blabla: Jak teraz wygląda w tym wątku moje rozwiązanie ?

ICSP: przez nazwę użytkownika: "debil".

blabla: Na przyszłość pisz .."kasuję" ( ICSP)

gov: Czy wczoraj Filipa też Ty zablokowałeś ?