 Witam was
Mam dziwne zadanie dla Was.
Głowię się już trochę, ale żadnego skutku. A dokładniej, piszę program CNC i potrzebuję znać
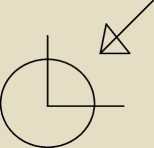
punkty na powierzchni zewnętrznej koła, w ćwiartce zaznaczonej na rysunku. Potrzebował bym
wzór na punkty x,y, rozłożonych od siebie o pewną równą odległość, zmieniających się od
promienia okręgu. Nie potrzebuję gotowca potrzebne naprowadzenie na trop.
pozdrawiam
Witam was
Mam dziwne zadanie dla Was.
Głowię się już trochę, ale żadnego skutku. A dokładniej, piszę program CNC i potrzebuję znać
punkty na powierzchni zewnętrznej koła, w ćwiartce zaznaczonej na rysunku. Potrzebował bym
wzór na punkty x,y, rozłożonych od siebie o pewną równą odległość, zmieniających się od
promienia okręgu. Nie potrzebuję gotowca potrzebne naprowadzenie na trop.
pozdrawiam
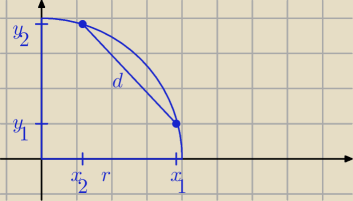 Czyli d masz dane, promień zmienny i chcesz wzorki na punkty (x1,y1) i (x2,y2) tak?
Czyli d masz dane, promień zmienny i chcesz wzorki na punkty (x1,y1) i (x2,y2) tak?
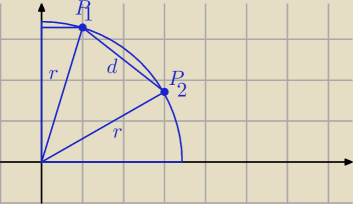 Z nudów coś tam popisałem, mam nadzieję, że o to chodziło, a jak nie o to, to może coś się z
tego przyda
Z nudów coś tam popisałem, mam nadzieję, że o to chodziło, a jak nie o to, to może coś się z
tego przyda  Ustalamy (x1,y1)
r = √x12 + y12
Rozważmy równanie okręgu o promieniu r i środku (0,0):
x2 + y2 = r2
oraz prostą przechodzącą przez punkt okręgu (x1,y1)
y = ax + b ⇒ y1 = ax1 + b ⇒ b = y1 − ax1
stąd
y = ax + y1 − ax1
Rozwiązujemy układ równań prostej i okręgu
x2 + (ax + y1 − ax1)2 = r2
x2 + a2x2 + y12 + a2x12 + 2axy1 − 2a2xx1 − 2ax1y1 = r2
x2(1 + a2) + x(2ay1 − 2a2x1) + y12 + a2x12 − 2ax1y1 − r2 = 0
Δ = (2ay1 − 2a2x1)2 − 4(1 + a2)(y12 + a2x12 − 2ax1y1 − r2) =
= 4a2y12 − 8a3x1y1 + 4a4x12
− 4(y12 + a2x12 − 2ax1y1 − r2 + a2y12 + a4x12 − 2a3x1y1 − a2r2) =
= − 4(y12 + a2x12 − 2ax1y1 − r2 − a2r2)
Przypomnijmy, że r = √x12 + y12 więc dalej mamy
= −4(− 2ax1y1 − x12 − a2y12) = 4(x1 + ay1)2
√Δ = 2(x1 + ay1)
Ustalamy (x1,y1)
r = √x12 + y12
Rozważmy równanie okręgu o promieniu r i środku (0,0):
x2 + y2 = r2
oraz prostą przechodzącą przez punkt okręgu (x1,y1)
y = ax + b ⇒ y1 = ax1 + b ⇒ b = y1 − ax1
stąd
y = ax + y1 − ax1
Rozwiązujemy układ równań prostej i okręgu
x2 + (ax + y1 − ax1)2 = r2
x2 + a2x2 + y12 + a2x12 + 2axy1 − 2a2xx1 − 2ax1y1 = r2
x2(1 + a2) + x(2ay1 − 2a2x1) + y12 + a2x12 − 2ax1y1 − r2 = 0
Δ = (2ay1 − 2a2x1)2 − 4(1 + a2)(y12 + a2x12 − 2ax1y1 − r2) =
= 4a2y12 − 8a3x1y1 + 4a4x12
− 4(y12 + a2x12 − 2ax1y1 − r2 + a2y12 + a4x12 − 2a3x1y1 − a2r2) =
= − 4(y12 + a2x12 − 2ax1y1 − r2 − a2r2)
Przypomnijmy, że r = √x12 + y12 więc dalej mamy
= −4(− 2ax1y1 − x12 − a2y12) = 4(x1 + ay1)2
√Δ = 2(x1 + ay1)
| −(2ay1 − 2a2x1) + 2(x1 + ay1) | ||
x' = | = | |
| 2(a2 + 1) |
| 2a2x1 + 2x1 | ||
= | = x1 (spodziewany punkt) | |
| 2(a2 + 1) |
| −(2ay1 − 2a2x1) − 2(x1 + ay1) | ||
x'' = | = | |
| 2(a2 + 1) |
| a2x1 − x1 − 2ay1 | ||
= | = x2 | |
| a2 + 1 |
| a2x1 − x1 − 2ay1 | ||
y2 = a * | + y1 − ax1 = | |
| a2 + 1 |
| a3x1 − ax1 − 2a2y1 + a2y1 − a3x1 + y1 − ax1 | ||
= | = | |
| a2 + 1 |
| − 2ax1 − a2y1+ y1 | ||
= | ||
| a2 + 1 |
| a2x1 − x1 − 2ay1 | ||
x1 − | = | |
| a2 + 1 |
| a2x1 + x1 − a2x1 + x1 + 2ay1 | |
= | |
| a2 + 1 |
| 2x1 + 2ay1 | |
| a2 + 1 |
| − 2ax1 − a2y1+ y1 | ||
y1 − | = | |
| a2 + 1 |
| 2a2y1 + 2ax1 | |
| a2 + 1 |
| 4(x1 + ay1)2 + 4a2(ay1 + x1)2 | ||
(*) = | = | |
| (a2 + 1)2 |
| 4(x1 + ay1)2(1 + a2) | ||
= | = | |
| (a2 + 1)2 |
| 4(x1 + ay1)2 | ||
= | ||
| a2 + 1 |
| −8x1y1+ 2d√4x12 + 4y12 − 1 | ||
a1 = | = | |
| 2(4y12 − d2) |
| −4x1y1 + d√4x12 + 4y12 − 1 | ||
= | ||
| 4y12 − d2 |
| −8x1y1 − 2d√4x12 + 4y12 − 1 | ||
a2 = | = | |
| 2(4y12 − d2) |
| −4x1y1 − d√4x12 + 4y12 − 1 | |
| 4y12 − d2 |
| −4x1y1 + d√4r2 − 1 | ||
a1 = | ||
| 4y12 − d2 |








 udało się to ogarnąć
udało się to ogarnąć

