Ekstrema funkcji Klaudia:

	lnx
Obliczyć ekstrema funkcji g(x)=
	x

J: potrafisz obliczyć pochodną ?

Klaudia: tak potrafie zaraz napisze

Klaudia:

	(lnx')(x)−(lnx)(x')		1		−lnx
g'=		={		*x−lnx*1 } /x2=		( nie umiałam zrobić
	x2		x		x2

normalnego ułamka w środku xD)

J:

	1   *x − lnx x		1 − lnx
nie tak .... f'(x) =		=		,
	x2		x2

teraz pytanie, kiedy pochodna sie zeruje

Klaudia: a no o 1 zapomniałam kiedy x=0 ?

J: nie pisz takich bzdur ... liczba 0 nie należy do dziedziny D = R₊ rozwiąż równanie: 1 − lnx = 0

Klaudia: −lnx=−1 lnx=1

J: no i kiedy lnx = 1 ? ( skorzystaj z definicji logarytmu )

Klaudia: x=e x≈2,72

J: wystarczy: x = e , tutaj może byc ekstremum ,ale nie musi .. warunek zmiana znaku pochodnej w punkcie x = e potrafisz naszkicować wykres: f(x) = − lnx + 1 ?

Klaudia: no właśnie nie umiem narysować

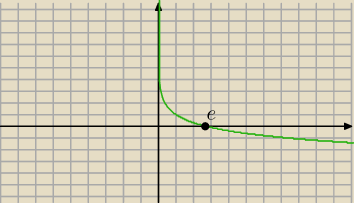
J: to jest rysunek ... zmienia znak pochodna, czy nie ? inne wyjście ... liczysz drugą pochodną i badasz jej znak w punkcie x = e

Klaudia: a co jak bym policzyła metodą Hospitala będzie to wtedy łatwiejsze? pochodna wychodzi wtedy =0

Klaudia: ale w sensie że jak zmienia znak?

J: reguła [H] dotyczy liczenia granic , a nie drugiej pochodnej .. jaki ma znak na lewo od e , a jaki na prawo od e ?

Klaudia: no tak mój błąd. na lewo od e ma + na prawo ma −

J: jak pochodna jest dodatnia to funkcja jest ? ( rosnąca, czy malejąca)

Klaudia: funkcja jest malejąca

J: odwrotnie ... jak f'(x) > 0 to jest rosnąca i odwrotnie ... tutaj funkcja najpierw rośnie aż do e , potem maleje ... czyli w x = e osiąga ...?

Klaudia: w x=e osiaga maximum

J: ano właśnie ... .dla wprawy policz drugą pochodną i powinna być ujemna dla x = e (jeśli druga pochodna jest ujemna to funkcja ma maksimum)

Klaudia:

	1
tak wychodzi ujemna −
	x

J:

	1		1
ściślej ...f"(x) = −		.. .i dla x = e f"(e) = −		< 0
	x2		e2

Klaudia: ok dzięki za pomoc