` asd: ∫∫xdxdy x∊[0,2] y∊[0,2] Jak takie coś zinterpretować graficznie ?

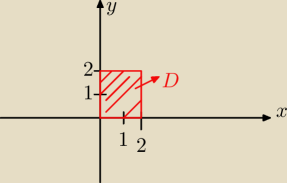
kyrtap: Obszar D: x∊[0,2] y∊[0,2]

asd: Ok, a w przypadku gdyby funkcja pod całką była taka (1−x) przedział taki sam ? To czym się sugerować, żeby poprawnie to narysować ?

kyrtap: jak byś miał ∫∫(1−x)dxdy?

asd: Tak, dokładnie nie wiem po prostu czym wspierać przy rysowaniu ?

kyrtap: Całka ∫∫xdxdy wskazuje co masz obliczyć Natomiast x∊[0,2] y∊[0,2] określa twój obszar całkowania czyli x od 0 do 2 a y od 0 do 2

Mila: Obszar całkowania masz podany przy całce podwójnej. Rysujesz to, co podają w treści, następnie ustalasz granice całkowania i liczysz całkę. W twoim przypadku: ₀∫²[₀∫²xdx]dy = to łatwy przypadek, granice stałe II przypadek podany przez 22:27 Ponieważ nie zmieniłeś obszaru całkowania to tak: ₀∫²[₀∫²(1−x)dx]dy =

Karolina: Wynik wyszedł równy 0